题目内容
已知直线l、m、n与平面α、β,给出下列四个命题:
①若m∥l,n∥l,则m∥n;
②若m⊥α,m∥β,则α⊥β;
③若m∥α,n∥α,则m∥n;
④若m⊥β,α⊥β,则m∥α;
其中假命题是( )
①若m∥l,n∥l,则m∥n;
②若m⊥α,m∥β,则α⊥β;
③若m∥α,n∥α,则m∥n;
④若m⊥β,α⊥β,则m∥α;
其中假命题是( )
| A、① | B、② | C、③ | D、③④ |
考点:平面与平面之间的位置关系
专题:空间位置关系与距离
分析:根据空间直线和平面平行或垂直的性质分别进行判断即可.
解答:
解:①若m∥l,n∥l,则根据公理4可知m∥n成立;
②若m⊥α,m∥β,则α⊥β成立;
③若m∥α,n∥α,则m∥n不一定成立;
④若m⊥β,α⊥β,则m∥α或m?α,故④错误;
故③④是假命题.
故选:D
②若m⊥α,m∥β,则α⊥β成立;
③若m∥α,n∥α,则m∥n不一定成立;
④若m⊥β,α⊥β,则m∥α或m?α,故④错误;
故③④是假命题.
故选:D
点评:本题主要考查命题的真假判断,根据空间直线和平面之间的位置关系是解决本题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
函数f(x)=x3-3x的单调递减区间是( )
| A、(∞,-1) |
| B、(1,+∞) |
| C、(-∞,-1)∪(1,+∞) |
| D、(-1,1) |
已知m,n是不重合的两条直,α,β是不重合的两个平面.则以下结论正确的是( )
| A、若α⊥β,m⊥α,则m∥β |
| B、若m∥α,m⊥n,则n⊥α |
| C、若m⊥α,m⊥β,则α∥β |
| D、若m∥α,m?β,则α∥β |
若实数x,y满足约束条件
,则z=x+y的最大值是4,则a=( )
|
| A、2 | B、3 | C、3或1 | D、4 |
 如图,在长方体ABCD-A1B1C1D1中,E、H分别是棱A1B1、C1D1上的点(点E 与B1不重合),且EH∥A1D1;过EH的平面与棱BB1、CC1相交,交点分别为F、G.
如图,在长方体ABCD-A1B1C1D1中,E、H分别是棱A1B1、C1D1上的点(点E 与B1不重合),且EH∥A1D1;过EH的平面与棱BB1、CC1相交,交点分别为F、G.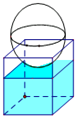 如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为
如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为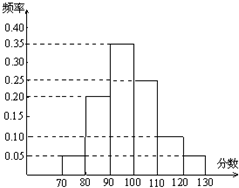 某校高三文科分为四个班.高三数学调研测试后,随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.
某校高三文科分为四个班.高三数学调研测试后,随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人. 已知ABCD为正方形,P是ABCD所成平面外一点,P在平面ABCD上的射影恰好是正方形的中心O.Q是CD的中点.
已知ABCD为正方形,P是ABCD所成平面外一点,P在平面ABCD上的射影恰好是正方形的中心O.Q是CD的中点.