题目内容
若实数x、y满足
，则S=2x+y的最大值为（ ）
|
| A、3 | B、2 | C、6 | D、7 |
考点：简单线性规划
专题：不等式的解法及应用
分析：由约束条件作出可行域，数形结合得到最优解，求出最优解的坐标，代入目标函数得答案．
解答：
解：由约束条件
正常可行域如图，
化目标函数S=2x+y为y=-2x+S，
由图可知，当直线y=-2x+S过B（2，3）时，S有最大值，为2×2+3=7．
故选：D．
|
化目标函数S=2x+y为y=-2x+S，
由图可知，当直线y=-2x+S过B（2，3）时，S有最大值，为2×2+3=7．
故选：D．
点评：本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
已知m，n是不重合的两条直，α，β是不重合的两个平面．则以下结论正确的是（ ）
| A、若α⊥β，m⊥α，则m∥β |
| B、若m∥α，m⊥n，则n⊥α |
| C、若m⊥α，m⊥β，则α∥β |
| D、若m∥α，m?β，则α∥β |
若实数x，y满足约束条件
，则z=x+y的最大值是4，则a=（ ）
|
| A、2 | B、3 | C、3或1 | D、4 |
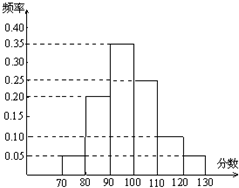某校高三文科分为四个班．高三数学调研测试后，随机地在各班抽取部分学生进行测试成绩统计，各班被抽取的学生人数恰好成等差数列，人数最少的班被抽取了22人．抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示，其中120～130（包括120分但不包括130分）的频率为0.05，此分数段的人数为5人．已知焦点在x轴上的椭圆
+
2=1的离心率是e=
，则a的值为（ ）
| x2 |
| a2 |
| y |
| 9 |
| 1 |
| 2 |
A、2
| ||
B、
| ||
C、3
| ||
| D、12 |
经过直线l1：x-6y+4=0和直线l2：2x+y=5的交点，并且与直线l2垂直的直线方程是（ ）
| A、x-2y=0 |
| B、x+2y=0 |
| C、x+2y-4=0 |
| D、x-2y-4=0 |