题目内容
已知cos(π+α)=
,π<α<2π,则sin2α的值是( )
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:二倍角的正弦
专题:三角函数的求值
分析:由条件利用诱导公式求得cosα的值,再利用同角三角函数的基本关系求得sinα,从而利用二倍角公式求得sin2α=2sinαcosα 的值.
解答:
解:∵cos(π+α)=
=-cosα,∴cosα=-
.
再根据π<α<2π,可得sinα=-
,
∴sin2α=2sinαcosα=2(-
)(-
)=
,
故选:D.
| 1 |
| 3 |
| 1 |
| 3 |
再根据π<α<2π,可得sinα=-
2
| ||
| 3 |
∴sin2α=2sinαcosα=2(-
2
| ||
| 3 |
| 1 |
| 3 |
4
| ||
| 9 |
故选:D.
点评:本题主要考查同角三角函数的基本关系,诱导公式、二倍角公式的应用,属于中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
函数f(x)=sin2(x-
)在[0,π]上的图象大致是( )
| π |
| 3 |
A、 |
B、 |
C、 |
D、 |
已知等差数列{an}中,am=k,ak=m,(m≠k),则am+k=( )
| A、m-k | B、m+k |
| C、-(m+k) | D、0 |
一个物体的运动方程是s=2t2+at+1,该物体在t=1时的瞬时速度为3,则a=( )
| A、1 | B、0 | C、-1 | D、7 |
函数y=
x2-1所对应的曲线在点(-
,
)处的切线的倾斜角为( )
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
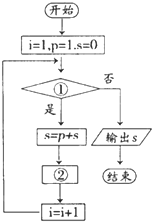 给出15个数:1,2,4,7,11,…,要计算这15个数的和,现给出解决该问题的程序框图(如图所示),那么框图中判断框①处和执行框②处应分别填入( )
给出15个数:1,2,4,7,11,…,要计算这15个数的和,现给出解决该问题的程序框图(如图所示),那么框图中判断框①处和执行框②处应分别填入( )| A、i≤16?; p=p+i-1 |
| B、i≤14?; p=p+i+1 |
| C、i≤15?; p=p+i+1 |
| D、i≤15?; p=p+i |
以下不等式不正确的是( )
A、tan(-
| ||||
B、sin(-
| ||||
C、cos(-
| ||||
D、tan(-
|
由正数组成的等比数列{an}满足:a4a8=9,则a5,a7的等比中项为( )
| A、±3 | B、3 | C、±9 | D、9 |