题目内容
17.某几何体的三视图如图所示,则该几何体的表面积是( )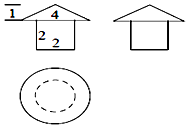
| A. | (6+2$\sqrt{5}$)π | B. | (8+2$\sqrt{5}$)π | C. | (9+2$\sqrt{5}$)π | D. | (10+2$\sqrt{5}$)π |
分析 由已知中的三视图,可知该几何体是由圆锥和圆柱组合而成.其表面等于圆锥和圆柱表面积减去2个圆柱底面积.
解答 解:由三视图可知,圆锥的底面半径2,高是1,母线为$\sqrt{5}$,其表面积S表=πr(l+r)=4π+2$\sqrt{5}$π;
圆柱底面半径1,高是2,底面的面积为:π,其表面积为:S表=2πr(h+r)=4π
那么该几何体的表面积为:8π+2$\sqrt{5}$π.
故选:B.
点评 本题考查的知识点是三视图的认识,求其表面积,解决本题的关键是知道该几何体的形状和组成才能正确计算其表面积.属于基础题.

练习册系列答案
相关题目
5.中央电视台为了调查近三年的春晚节目中各类节目的受欢迎程度,用分层抽样的方法,从2014年至2016年春晚的50个歌舞类节目,40个戏曲类节目,30个小品类节目中抽取样本进行调查,若样本中的歌舞类和戏曲类节目共有27个,则样本容量为( )
| A. | 36 | B. | 35 | C. | 32 | D. | 30 |
2.设实数x,y满足条件$\left\{\begin{array}{l}{x-y+2≥0}\\{2x-y-4≤0}\\{x≥0,y≥0}\end{array}\right.$,若目标函数z=ax+by(a>0,b>0)的最大值为 12,则$\frac{3}{a}$+$\frac{4}{b}$的最小值为( )
| A. | $\frac{49}{6}$ | B. | $\frac{25}{6}$ | C. | $\frac{8}{3}$ | D. | 4 |
9.设全集U=R,集合A={x|x≥0},B={x|(x-3)(x+1)<0},则(∁UA)∩B=( )
| A. | {x|-3<x<0} | B. | {x|-1<x<0} | C. | {x|0<x<1} | D. | {x|0<x<3} |
6.3x=4,则x=( )
| A. | log43 | B. | 64 | C. | log34 | D. | 81 |