题目内容
以下命题中,真命题有( )
①已知平面α、β和直线m,若m∥α且α⊥β,则m⊥β.
②“若x2<1,则-1<x<1”的逆否命题是“若x<-1或x>1,则x2>1”.
③已知△ABC,D为AB边上一点,若
=2
,
=
+λ
,则λ=
.
④极坐标系下,直线ρcos(θ-
)=
与圆ρ=
有且只有1个公共点.
①已知平面α、β和直线m,若m∥α且α⊥β,则m⊥β.
②“若x2<1,则-1<x<1”的逆否命题是“若x<-1或x>1,则x2>1”.
③已知△ABC,D为AB边上一点,若
| AD |
| DB |
| CD |
| 1 |
| 3 |
| CA |
| CB |
| 2 |
| 3 |
④极坐标系下,直线ρcos(θ-
| π |
| 4 |
| 2 |
| 2 |
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:命题的真假判断与应用,必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据空间线面关系的判断与几何特征,可判断①;写出原命题的逆否命题可判断②;根据三点共线的向量表示法,可判断③;分析直线与圆的位置关系,可判断④.
解答:
解:若m∥α且α⊥β,则m与β的关系不能确定,故①错误;
“若x2<1,则-1<x<1”的逆否命题是“若x≤-1或x≥1,则x2≥1”,故②错误;
若
=2
,则A,B,D三点共线,若
=
+λ
,则λ+
=1.即λ=
,故③正确;
极坐标系下,直线ρcos(θ-
)=
与圆ρ=
相切,故只有一个公共点,故④正确;
故真命题有2个,
故选:C
“若x2<1,则-1<x<1”的逆否命题是“若x≤-1或x≥1,则x2≥1”,故②错误;
若
| AD |
| DB |
| CD |
| 1 |
| 3 |
| CA |
| CB |
| 1 |
| 3 |
| 2 |
| 3 |
极坐标系下,直线ρcos(θ-
| π |
| 4 |
| 2 |
| 2 |
故真命题有2个,
故选:C
点评:本题以命题的真假判断为载体,考查了空间线面关系,四种命题,三点共线的向量表示法,及直线与圆的位置关系,难度不大,属于基础题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
已知复数z=3+4i,
表示复数z的共轭复数,则复数
在付平面内对应的点在( )
. |
| z |
| ||
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若条件p:(x-3)(x-4)=0,条件q:x-3=0,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分条件也不必要条件 |
已知实数x,y满足
,则2x-y的最小值是( )
|
| A、-3 | B、0 | C、6 | D、10 |
给出的图象中可能为函数f(x)=x4+ax3+cx2+bx+d(a,b,c,d∈R)的图象是( )
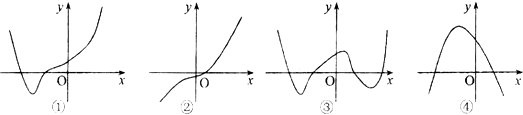

| A、①③ | B、①② | C、③④ | D、②④ |
已知函数f(x)=ax3+bx+2013,若f(2014)=4025,则f(-2014)的值为( )
| A、1 | B、-4025 |
| C、-2013 | D、2014 |
 某小学数学组组织了“自主招生选拔赛”从参加考试的学生中抽出60名学生,将其成绩分为六组[40,50)[50,60),…[90,100],其部分频率分布直方图如图所示,观察图形,从成绩在[40,50)和[90,100]的学生中随即选两个人,则他们在同一分数段的概率是( )
某小学数学组组织了“自主招生选拔赛”从参加考试的学生中抽出60名学生,将其成绩分为六组[40,50)[50,60),…[90,100],其部分频率分布直方图如图所示,观察图形,从成绩在[40,50)和[90,100]的学生中随即选两个人,则他们在同一分数段的概率是( )