题目内容
若n=
8sinxdx,则(2-
)n展开式中不含x4项的其他各项系数的和为 .
| ∫ |
0 |
| x |
考点:定积分,二项式系数的性质
专题:计算题,二项式定理
分析:由定积分求出n的值,代入(2-
)n,求出二项展开式的通项;由x得系数确定r值,可求x4项的系数;再给二项式中的x赋值1,得到展开式中各项的系数的和;进而得到不含x4项的其他各项系数的和.
| x |
解答:
解:∵n=
8sinxdx=(-8cosx)
=-8cos
+8cos0=8,
(2-
)n=(2-
)8,
其展开式的通项为Tr+1=C8r28-r(-
)r=(-1)rC8r28-rx
,
令
=4得r=8
∴二项展开式中x4的系数为(-1)8C8828-8=1,
令(2-
)8中的x=1,
得到(2-
)8的展开式中各项系数的和为1,
故(2-
)n展开式中不含x4项的其他各项系数的和为0,
故答案为:0.
| ∫ |
0 |
| | |
0 |
| π |
| 2 |
(2-
| x |
| x |
其展开式的通项为Tr+1=C8r28-r(-
| x |
| r |
| 2 |
令
| r |
| 2 |
∴二项展开式中x4的系数为(-1)8C8828-8=1,
令(2-
| x |
得到(2-
| x |
故(2-
| x |
故答案为:0.
点评:本题考查了定积分,考查了二项式系数的性质,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
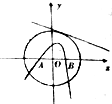 如图⊙O2:x2+y2=9,A(-2,0),B(2,0)为两个定点,l是⊙O的一条切线,若过A、B两点的抛物线以直线l为准线,则抛物线焦点的轨迹方程是
如图⊙O2:x2+y2=9,A(-2,0),B(2,0)为两个定点,l是⊙O的一条切线,若过A、B两点的抛物线以直线l为准线,则抛物线焦点的轨迹方程是