题目内容
给出的图象中可能为函数f(x)=x4+ax3+cx2+bx+d(a,b,c,d∈R)的图象是( )
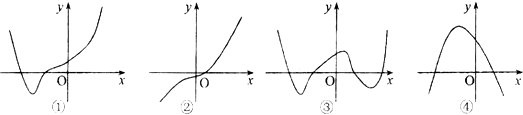

| A、①③ | B、①② | C、③④ | D、②④ |
考点:函数的图象
专题:分类讨论
分析:确定函数的图象,可由函数单调性的可能情况确定函数图象的形状,故可求出函数的导数,通过函数的导数研究函数的单调性,从而推测出函数图象的大致形状得出可能的图象是那几个,从而得到答案.
解答:
解:∵f(x)=x4+ax3+bx2+cx+d(a,b,c,d∈R)
∴f'(x)=4x3+3ax2+2bx+c
此函数相应方程的根可能有三个或两个或一个,
若方程可能的根有一个,如a,b,c都为0时,f'(x)=0的根只有一个,故函数值先负后正,故函数的图象是先减后增,符合条件的只有①
若方程可能的根有两个,函数有两个极值点,函数图象必是先减后增再减型,与题意不符,
若方程的根有三个,则函数有三个极值点,函数的单调性是先减后增再减再增型,考察②③④得③符合条件
综上讨论知,①③中的图象可能是函数的图象,
故选:A.
∴f'(x)=4x3+3ax2+2bx+c
此函数相应方程的根可能有三个或两个或一个,
若方程可能的根有一个,如a,b,c都为0时,f'(x)=0的根只有一个,故函数值先负后正,故函数的图象是先减后增,符合条件的只有①
若方程可能的根有两个,函数有两个极值点,函数图象必是先减后增再减型,与题意不符,
若方程的根有三个,则函数有三个极值点,函数的单调性是先减后增再减再增型,考察②③④得③符合条件
综上讨论知,①③中的图象可能是函数的图象,
故选:A.
点评:本题考查函数的图象,解题的关键是推测出函数图象的性质,由这些性质得出函数的图象的特征从而选出可能的图象的序号,本题借助导数研究函数的单调性与极值,比较抽象,有一定的难度.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
若(x-
)8展开式中含x2的项的系数为7,则a=( )
| 1 |
| ax |
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
在△ABC中,三个内角A、B、C成等差数列,则角A+C=( )
| A、30° | B、60° |
| C、90° | D、120° |
在复平面内,复数
对应的点位于( )
| 2+i |
| 2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
等差数列{an}中,已知a1+a3=6,a5+a7=14,则a20+a22=( )
| A、44 | B、56 | C、42 | D、40 |
已知函数f(x)=ax+
(a>1),则f(x)=0的根有( )
| x-2 |
| x+1 |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列关于向量若
,
的命题中,错误命题的是( )
| a |
| b |
A、若
| ||||||||||
B、若k∈R,k
| ||||||||||
C、若|
| ||||||||||
D、若
|