题目内容
已知等比数列{an}的前n项和为Sn,a1=3,且3S1,2S2,S3成等差数列.
(1)求数列{an}的通项公式;
(2)设bn=log3an,求Tn=b1b2-b2b3+b3b4-b4b5+…+b2n-1b2n-b2nb2n+1.
(1)求数列{an}的通项公式;
(2)设bn=log3an,求Tn=b1b2-b2b3+b3b4-b4b5+…+b2n-1b2n-b2nb2n+1.
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)由3S1,2S2,S3成等差数列,求得公比q,写出通项公式;
(Ⅱ)由(Ⅰ)知,bn=log3an=log33n=n,b2n-1b2n-b2nb2n+1=(2n-1)•2n-2n(2n+1)=-4n,利用分组求和,即可得出结论.
(Ⅱ)由(Ⅰ)知,bn=log3an=log33n=n,b2n-1b2n-b2nb2n+1=(2n-1)•2n-2n(2n+1)=-4n,利用分组求和,即可得出结论.
解答:
解:(Ⅰ)∵3S1,2S2,S3成等差数列,∴4S2=3S1+S3,
∴4(a1+a2)=3a1+(a1+a2+a3),即a3=3a2,∴公比q=3,
∴an=a1qn-1=3n.…(6分)
(Ⅱ)由(Ⅰ)知,bn=log3an=log33n=n,
∵b2n-1b2n-b2nb2n+1=(2n-1)•2n-2n(2n+1)=-4n,
∴Tn=b1b2-b2b3+b3b4-b4b5+…+b2n-1b2n-b2nb2n+1
=-4(1+2+3+…+n)=-4×
=-2n2-2n.…(12分)
∴4(a1+a2)=3a1+(a1+a2+a3),即a3=3a2,∴公比q=3,
∴an=a1qn-1=3n.…(6分)
(Ⅱ)由(Ⅰ)知,bn=log3an=log33n=n,
∵b2n-1b2n-b2nb2n+1=(2n-1)•2n-2n(2n+1)=-4n,
∴Tn=b1b2-b2b3+b3b4-b4b5+…+b2n-1b2n-b2nb2n+1
=-4(1+2+3+…+n)=-4×
| n(n+1) |
| 2 |
点评:本题主要考查了等差数列和等比数列的定义及性质,考查分组求和的方法及学生的运算能力,属中档题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
执行如图所示的程序框图,若输入的x,y∈R,那么输出的S的最大值为( )


| A、0 | B、1 | C、2 | D、3 |
在等差数列{an}中,已知a3+a9=16,则该数列前11项和S11=( )
| A、58 | B、88 |
| C、143 | D、176 |
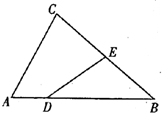 如图,在△ABC中,已知点D,E分别在边AB,BC上,且AB=4AD,BC=2BE.
如图,在△ABC中,已知点D,E分别在边AB,BC上,且AB=4AD,BC=2BE.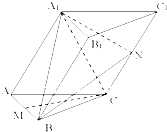 己知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧面A1ACC1为菱形,∠A1AC=60°,平面A1ACC1⊥平面ABC,M、N是AB,CC1的中点.
己知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧面A1ACC1为菱形,∠A1AC=60°,平面A1ACC1⊥平面ABC,M、N是AB,CC1的中点.