题目内容
已知函数f（x）=ln（
-x）（其中e为自然数对数的底数），则f（tan
）+2f（tanπ）+f（tan
）= ．
| e+x2 |
| π |
| 12 |
| 11π |
| 12 |
考点：函数奇偶性的性质,函数奇偶性的判断,对数的运算性质
专题：函数的性质及应用
分析：判断函数的奇偶性，然后求解表达式的值．
解答：
解：∵函数f（x）=ln（
-x），
∴f（-x）=ln（
+x）=-ln（
-x）=-f（x），函数是奇函数，
∵tan
=-tan
，
∴f（tan
）+2f（tanπ）+f（tan
）=2f（tanπ）=2f（0）=2ln
=1．
故答案为：1．
| e+x2 |
∴f（-x）=ln（
| e+x2 |
| e+x2 |
∵tan
| 11π |
| 12 |
| π |
| 12 |
∴f（tan
| π |
| 12 |
| 11π |
| 12 |
| e |
故答案为：1．
点评：本题考查函数的值的求法，函数的奇偶性的判断与应用，基本知识的考查．
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
i是虚数单位，复数
=（ ）
| 7+i |
| 3+4i |
| A、1-i | ||||
| B、-1+i | ||||
C、
| ||||
D、-
|
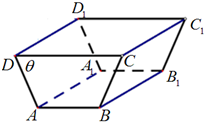某农户准备建一个水平放置的直四棱柱形储水窖（如图），其中直四棱柱的高AA1=10m，两底面ABCD，A1B1C1D1是高为2m，面积为10m2的等腰梯形，且∠ADC=θ（0＜θ＜
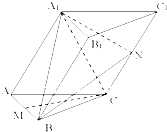己知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形，侧面A1ACC1为菱形，∠A1AC=60°，平面A1ACC1⊥平面ABC，M、N是AB，CC1的中点．已知集合U={-1，0，1}，A={1}，B⊆U，则B∩（∁UA）不可能为（ ）
| A、∅ | B、{0} |
| C、{-1，0} | D、{-1，0，1} |