题目内容
已知集合M={m|(m-6)(m-10)≤0,m∈N},若(x2-
)n(n∈M)的二项展开式中存在常数项,则n等于( )
| 1 |
| x3 |
| A、7 | B、8 | C、9 | D、10 |
考点:二项式系数的性质
专题:二项式定理
分析:在二项展开式的通项公式中,令x的幂指数等于0,求出n=
,r≤n,6≤n≤10,n∈N、r∈N,从而求得n的值.
| 5r |
| 2 |
解答:
解:由题意可得,M={m|6≤m≤10,m∈N }.
由于(x2-
)n(n∈M)的二项展开式的通项公式为 Tr+1=
•(-1)r•x2n-5r,
令2n-5r=0,求得n=
,r≤n,6≤n≤10,n∈N、r∈N.
∴r=4,n=10,
故选:D.
由于(x2-
| 1 |
| x3 |
| C | r m |
令2n-5r=0,求得n=
| 5r |
| 2 |
∴r=4,n=10,
故选:D.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
设
,
为非零向量,|
|=2|
|,两组向量
,
,
,
和
,
,
,
,均由2个
和2个
排列而成,若
•
+
•
+
•
+
•
所有可能取值中的最小值为4|
|2,则
与
的夹角为( )
| a |
| b |
| b |
| a |
| x1 |
| x2 |
| x3 |
| x4 |
| y1 |
| y2 |
| y3 |
| y4 |
| a |
| b |
| x1 |
| y1 |
| x2 |
| y2 |
| x3 |
| y3 |
| x4 |
| y4 |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
| D、0 |
已知复数z满足(3-4i)z=25,则z=( )
| A、-3-4i | B、-3+4i |
| C、3-4i | D、3+4i |
执行如图所示的程序框图,若输入的x,y∈R,那么输出的S的最大值为( )


| A、0 | B、1 | C、2 | D、3 |
i是虚数单位,复数
=( )
| 7+i |
| 3+4i |
| A、1-i | ||||
| B、-1+i | ||||
C、
| ||||
D、-
|
某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是( )
| A、0.8 | B、0.75 |
| C、0.6 | D、0.45 |
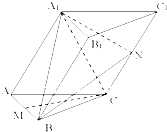 己知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧面A1ACC1为菱形,∠A1AC=60°,平面A1ACC1⊥平面ABC,M、N是AB,CC1的中点.
己知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧面A1ACC1为菱形,∠A1AC=60°,平面A1ACC1⊥平面ABC,M、N是AB,CC1的中点.