题目内容
已知a、b、c分别为△ABC三个内角A、B、C的对边，若acosC+
asinC-b=0，则∠A= ．
| 3 |
考点：余弦定理
专题：三角函数的求值
分析：已知等式利用正弦定理化简，再利用两角和与差的正弦函数公式化简，整理后求出tanA的值，即可确定出A的度数．
解答：
解：将acosC+
asinC-b=0，利用正弦定理化简得：sinAcosC+
sinAsinC-sinB=0，
即sinAcosC+
sinAsinC-sin（A+C）=sinAcosC+
sinAsinC-sinAcosC-cosAsinC=0，
整理得：
sinAsinC=cosAsinC，
∵sinC≠0，△ABC三个内角A、B、C，
∴
sinA=cosA，即tanA=
，
则A=
．
故答案为：
| 3 |
| 3 |
即sinAcosC+
| 3 |
| 3 |
整理得：
| 3 |
∵sinC≠0，△ABC三个内角A、B、C，
∴
| 3 |
| ||
| 3 |
则A=
| π |
| 6 |
故答案为：
| π |
| 6 |
点评：此题考查了正弦定理，两角和与差的正弦函数公式，以及特殊角的三角函数值，熟练掌握定理及公式是解本题的关键．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
某地区空气质量监测资料表明，一天的空气质量为优良的概率是0.75，连续两天为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是（ ）
| A、0.8 | B、0.75 |
| C、0.6 | D、0.45 |
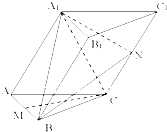己知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形，侧面A1ACC1为菱形，∠A1AC=60°，平面A1ACC1⊥平面ABC，M、N是AB，CC1的中点．