题目内容
已知数列{an}的前n项和Sn,满足:a1=1,Sn-2Sn-1=1,n∈N*,且n≥2.
(1)求证:数列{an}是等比数列;
(2)已知cn=
(n∈N*),数列{cn}的前n项和Tn,若存在正整数M,m,使m≤Tn<M对任意正整数n恒成立,求M,m的值.
(1)求证:数列{an}是等比数列;
(2)已知cn=
| n |
| an |
考点:数列的求和,等比关系的确定
专题:等差数列与等比数列
分析:(1)利用an与sn的关系,两式作差即得结论;
(2)利用错位相减法求得数列{cn}的前n项和Tn,再利用数列的增减性及放缩法求得Tn的最小值、最大值,即可得证.
(2)利用错位相减法求得数列{cn}的前n项和Tn,再利用数列的增减性及放缩法求得Tn的最小值、最大值,即可得证.
解答:
解:(1)当n≥2时,由
两式相减得an+1-2an=0,
又当n=2时,a2=2,
所以
=2(n∈N*),
所以{an}是以1为首项,2为公比的等比数列.
(2)由(1)得an=2n-1,∴cn=n×(
)n-1,
∴Tn=1×(
)0+2×(
)1+3×(
)2+…+(n-1)×(
)n-2+n×(
)n-1
∴
Tn=1×(
)1+2×(
)2+3×(
)3+…+(n-1)×(
)n-1+n×(
)n
两式相减得
Tn=(
)0+(
)1+(
)2+…+(
)n-1-n×(
)n=2-(n+2)×(
)n
∴Tn=4-(n+2)×(
)n-1<4,
所以M可以取大于等于4的任意整数,
又∵Tn+1-Tn=(n+1)×(
)n>0∴Tn≥T1=1,
综上,存在正整数M,m,使得m≤Tn<M对任意正整数n恒成立,其中m=1,M≥4且M∈N.
|
又当n=2时,a2=2,
所以
| an+1 |
| an |
所以{an}是以1为首项,2为公比的等比数列.
(2)由(1)得an=2n-1,∴cn=n×(
| 1 |
| 2 |
∴Tn=1×(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
两式相减得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴Tn=4-(n+2)×(
| 1 |
| 2 |
所以M可以取大于等于4的任意整数,
又∵Tn+1-Tn=(n+1)×(
| 1 |
| 2 |
综上,存在正整数M,m,使得m≤Tn<M对任意正整数n恒成立,其中m=1,M≥4且M∈N.
点评:本题主要考查利用公式法求数列的通项公式及数列求和的方法错位相减法的运用,考查学生的运算能力及恒成立问题的转化能力,属中档题.

练习册系列答案
相关题目
i是虚数单位,复数
=( )
| 7+i |
| 3+4i |
| A、1-i | ||||
| B、-1+i | ||||
C、
| ||||
D、-
|
某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是( )
| A、0.8 | B、0.75 |
| C、0.6 | D、0.45 |
对任意x,y∈R,|x-1|+|x|+|y-1|+|y+1|的最小值为( )
| A、1 | B、2 | C、3 | D、4 |
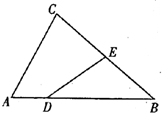 如图,在△ABC中,已知点D,E分别在边AB,BC上,且AB=4AD,BC=2BE.
如图,在△ABC中,已知点D,E分别在边AB,BC上,且AB=4AD,BC=2BE.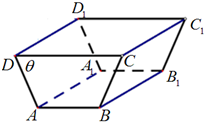 某农户准备建一个水平放置的直四棱柱形储水窖(如图),其中直四棱柱的高AA1=10m,两底面ABCD,A1B1C1D1是高为2m,面积为10m2的等腰梯形,且∠ADC=θ(0<θ<
某农户准备建一个水平放置的直四棱柱形储水窖(如图),其中直四棱柱的高AA1=10m,两底面ABCD,A1B1C1D1是高为2m,面积为10m2的等腰梯形,且∠ADC=θ(0<θ<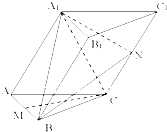 己知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧面A1ACC1为菱形,∠A1AC=60°,平面A1ACC1⊥平面ABC,M、N是AB,CC1的中点.
己知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧面A1ACC1为菱形,∠A1AC=60°,平面A1ACC1⊥平面ABC,M、N是AB,CC1的中点.