题目内容
设集合A={x|
＞0}，B={x|x2-（a+2）x+2a＜0}，若A∪B=A，求实数a的取值范围．
| x-4 |
| 1-x |
考点：并集及其运算
专题：集合
分析：先化简求出集合A，对参数a进行分类讨论，根据A是B的子集建立不等关系，解之即可求出参数a的范围．
解答：
解：∵A∪B=B，∴B⊆A
∵
＞0
∴1＜x＜4
集合A={x|1＜x＜4}
∵A∪B=A，
∴B⊆A，
B={x|x2-（a+2）x+2a＜0}={x|（x-a）（x-2）＜0}，
（1）当a＞2时，B={x|2＜x＜a}，
∵B⊆A
∴a≤4，
故2＜a≤4
（2）a=2时，B=Φ满足B⊆A，
（3）当a＜2时，B={x|a＜x＜2}，∵B⊆A∴a≥1，故1≤a＜2
综上：1≤a≤4
∵
| x-4 |
| 1-x |
∴1＜x＜4
集合A={x|1＜x＜4}
∵A∪B=A，
∴B⊆A，
B={x|x2-（a+2）x+2a＜0}={x|（x-a）（x-2）＜0}，
（1）当a＞2时，B={x|2＜x＜a}，
∵B⊆A
∴a≤4，
故2＜a≤4
（2）a=2时，B=Φ满足B⊆A，
（3）当a＜2时，B={x|a＜x＜2}，∵B⊆A∴a≥1，故1≤a＜2
综上：1≤a≤4
点评：本题考查了集合的运算、不等式的解法，属于基础题．
练习册系列答案
相关题目
设
，
为非零向量，|
|=2|
|，两组向量
，
，
，
和
，
，
，
，均由2个
和2个
排列而成，若
•
+
•
+
•
+
•
所有可能取值中的最小值为4|
|2，则
与
的夹角为（ ）
| a |
| b |
| b |
| a |
| x1 |
| x2 |
| x3 |
| x4 |
| y1 |
| y2 |
| y3 |
| y4 |
| a |
| b |
| x1 |
| y1 |
| x2 |
| y2 |
| x3 |
| y3 |
| x4 |
| y4 |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
| D、0 |
某地区空气质量监测资料表明，一天的空气质量为优良的概率是0.75，连续两天为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是（ ）
| A、0.8 | B、0.75 |
| C、0.6 | D、0.45 |
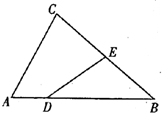如图，在△ABC中，已知点D，E分别在边AB，BC上，且AB=4AD，BC=2BE．
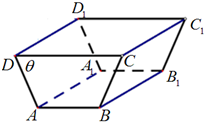某农户准备建一个水平放置的直四棱柱形储水窖（如图），其中直四棱柱的高AA1=10m，两底面ABCD，A1B1C1D1是高为2m，面积为10m2的等腰梯形，且∠ADC=θ（0＜θ＜
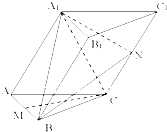己知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形，侧面A1ACC1为菱形，∠A1AC=60°，平面A1ACC1⊥平面ABC，M、N是AB，CC1的中点．