题目内容
若数列{an}满足点(
,
)(n∈N*)在函数f(x)=x+2n的图象上,且a1=4.
(Ⅰ)求数列{an}的通项公式.
(Ⅱ)求证:
≤
+
+…+
<2.
| 1 |
| an |
| 1 |
| an+1 |
(Ⅰ)求数列{an}的通项公式.
(Ⅱ)求证:
| 4 |
| 3 |
| a1a2 |
| a2a3 |
| anan+1 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)由题意得
-
=2n,利用累加法求得通项公式;
(Ⅱ)由(Ⅰ)得
=
=2(
-
),利用裂项法求和,放缩即得结论.
| 1 |
| an+1 |
| 1 |
| an |
(Ⅱ)由(Ⅰ)得
| anan+1 |
| 4 |
| (2n-1)(2n+1) |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
解答:
解:(Ⅰ)由题意得
=
+2n,
∴
-
=2n,
-
=2(n-1),…
-
=2×2,
-
=2×1,
∴累加得
-
=n2-n,即
=
+n2-n,又a1=4,
∴an=
.
(Ⅱ)由(Ⅰ)得
=
=2(
-
),
∴
+
+…+
=2(1-
+
-
+…+
-
)=2(1-
)=
<
=2
又
≥
=
,
∴
≤
+
+…+
<2.
| 1 |
| an+1 |
| 1 |
| an |
∴
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| an |
| 1 |
| an-1 |
| 1 |
| a3 |
| 1 |
| a2 |
| 1 |
| a2 |
| 1 |
| a1 |
∴累加得
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| an |
| 1 |
| a1 |
∴an=
| 4 |
| (2n-1)2 |
(Ⅱ)由(Ⅰ)得
| anan+1 |
| 4 |
| (2n-1)(2n+1) |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴
| a1a2 |
| a2a3 |
| anan+1 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2n+1 |
| 4n |
| 2n+1 |
| 4n |
| 2n |
又
| 4n |
| 2n+1 |
| 4n |
| 2n+n |
| 4 |
| 3 |
∴
| 4 |
| 3 |
| a1a2 |
| a2a3 |
| anan+1 |
点评:本题主要考查数列通项公式的求法累加法及数列求和的裂项法,考查学生的运算能力,属中档题.

练习册系列答案
相关题目
已知复数z满足(3-4i)z=25,则z=( )
| A、-3-4i | B、-3+4i |
| C、3-4i | D、3+4i |
对任意x,y∈R,|x-1|+|x|+|y-1|+|y+1|的最小值为( )
| A、1 | B、2 | C、3 | D、4 |
i是虚数单位,复数
的虚部为( )
| -2i |
| 1+i |
| A、2 | B、-1 | C、1 | D、-2 |
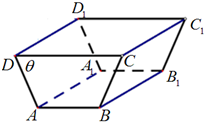 某农户准备建一个水平放置的直四棱柱形储水窖(如图),其中直四棱柱的高AA1=10m,两底面ABCD,A1B1C1D1是高为2m,面积为10m2的等腰梯形,且∠ADC=θ(0<θ<
某农户准备建一个水平放置的直四棱柱形储水窖(如图),其中直四棱柱的高AA1=10m,两底面ABCD,A1B1C1D1是高为2m,面积为10m2的等腰梯形,且∠ADC=θ(0<θ<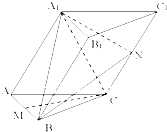 己知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧面A1ACC1为菱形,∠A1AC=60°,平面A1ACC1⊥平面ABC,M、N是AB,CC1的中点.
己知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧面A1ACC1为菱形,∠A1AC=60°,平面A1ACC1⊥平面ABC,M、N是AB,CC1的中点.