Question

已知点A（-3，0），B（0，3），若点P在圆x²+y²-2x=0上运动，则△PAB面积的最小值为

 

．

Answer 1

考点：圆方程的综合应用

专题：直线与圆

分析：利用数形结合，利用直线和圆的位置关系即可得到结论．

解答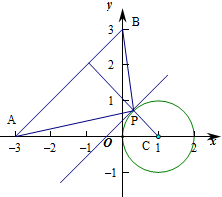： 解：圆的标准方程为（x-1）²+y²=1，圆心C（1，0），半径r=1，
当过P的直线和AB平行时，△PAB的面积最小，
∵A（-3，0），B（0，3），
∴AB的方程为

x

-3

+

y

3

=1，即x-y+3=0，
此时圆心C到直线AB的距离d=

|1-0+3|

2

=

4

2

=2

2

，
则△PAB的边长AB=

32+(-3)2

=3

2

，
AB边上的高h=d-r=2

2

-1，
则△PAB面积S=

1

2

×3

2

×(2

2

-1)=6-

3 2

2

，
故答案为：6-

3 2

2

点评：本题主要考查直线和圆的位置关系的应用，利用数形结合即可得到结论．