题目内容
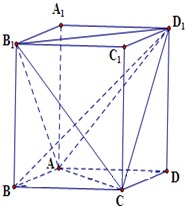 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AB=1,AA1=
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AB=1,AA1=
| ||
| 2 |
考点:直线与平面垂直的判定
专题:空间位置关系与距离
分析:连结BD,交AC于O,连结B1O交D1B于E,根据余弦定理求得BD,根据BO∥B1D1,确定比例关系分别求得BE,OE,OB,利用勾股定理证明出BD1⊥OB1,通过证明出AC⊥面BDD1,推断出AC⊥BD1,最后通过线面垂直的判定定理证明出BD1⊥平面AB1C.
解答:
证明:连结BD,交AC于O,连结B1O交D1B于E,
∵BO∥B1D1,
∴
=
=
,
由余弦定理BD=
=
,
∴OB=
BD=
,
OB1=
=
,
∴OE=
OB1=
,
BD1=
=
,BE=
BD1=
,
∴BE2+OE2=BO2,即BD1⊥OB1,
∵底面ABCD为菱形,
∴BD⊥AC,
∵DD1⊥AC,
∴AC⊥面BDD1,
∵BD1?面BDD1,
∴AC⊥BD1,
∵AC?平面AB1C,OB1?平面AB1C,AC∩OB1=O,
∴BD1⊥平面AB1C.
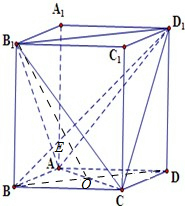
∵BO∥B1D1,
∴
| OE |
| B1E |
| BE |
| ED1 |
| 1 |
| 2 |
由余弦定理BD=
| 1+1-2cos120°×1×1 |
| 3 |
∴OB=
| 1 |
| 2 |
| ||
| 2 |
OB1=
|
| 3 |
| 2 |
∴OE=
| 1 |
| 3 |
| 1 |
| 2 |
BD1=
3+
|
3
| ||
| 2 |
| 1 |
| 3 |
| ||
| 2 |
∴BE2+OE2=BO2,即BD1⊥OB1,
∵底面ABCD为菱形,
∴BD⊥AC,
∵DD1⊥AC,
∴AC⊥面BDD1,
∵BD1?面BDD1,
∴AC⊥BD1,
∵AC?平面AB1C,OB1?平面AB1C,AC∩OB1=O,
∴BD1⊥平面AB1C.

点评:本题主要考查了线面垂直的判定定理的应用.证明的关键是找到同一面内同时垂直的两条相交的线.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
已知函数f(x)=
x3+ax2-4在区间(0,2)上是减函数,则a的范围是( )
| 1 |
| 3 |
| A、(-∞,3] |
| B、[-1,+∞) |
| C、[3,+∞) |
| D、(-∞,-1] |
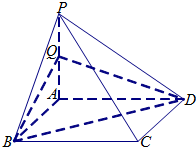 如图所示,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧棱PA⊥底面ABCD,且PA=2,Q是PA的中点.
如图所示,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧棱PA⊥底面ABCD,且PA=2,Q是PA的中点.