题目内容
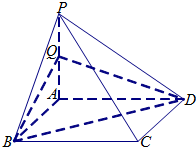 如图所示,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧棱PA⊥底面ABCD,且PA=2,Q是PA的中点.
如图所示,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧棱PA⊥底面ABCD,且PA=2,Q是PA的中点.(Ⅰ)证明:PC∥平面BDQ;
(Ⅱ)求三棱锥Q-BAD的体积.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(I)连接AC交BD于O,再连接OE,根据中位线定理可得到PC∥OE,再由线面平行的判定定理可证明PC∥OE,得证.
(II)先根据PA⊥平面ABCD确定QA为棱锥Q-BAD的高,进而根据棱锥的体积公式可求出四棱锥Q-BAD的体积.
(II)先根据PA⊥平面ABCD确定QA为棱锥Q-BAD的高,进而根据棱锥的体积公式可求出四棱锥Q-BAD的体积.
解答:
证明:(I)连接AC交BD于O,连接OE.
∵四边形ABCD是正方形,
∴O是AC的中点.
又∵E是PA的中点,
∴PC∥OE.
∵PC?平面BDE,OE?平面BDE
∴PC∥平面BDE.…(6分)
(II)∵侧棱PA⊥底面ABCD,且PA=2,Q是PA的中点.
∴棱锥Q-BAD的高QA=1,
又∵底面ABCD是边长为2的正方形,
∴棱锥Q-BAD的底面面积S△BAD=2,
∴VQ-BAD=
×S△BAD×QA=
×2×1=
.…(13分)
∵四边形ABCD是正方形,
∴O是AC的中点.
又∵E是PA的中点,
∴PC∥OE.
∵PC?平面BDE,OE?平面BDE
∴PC∥平面BDE.…(6分)
(II)∵侧棱PA⊥底面ABCD,且PA=2,Q是PA的中点.
∴棱锥Q-BAD的高QA=1,
又∵底面ABCD是边长为2的正方形,
∴棱锥Q-BAD的底面面积S△BAD=2,
∴VQ-BAD=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
点评:本题主要考查棱锥的体积公式和线面平行的判定定理的应用.考查对定理的掌握情况和对基础知识的综合运用.

练习册系列答案
相关题目
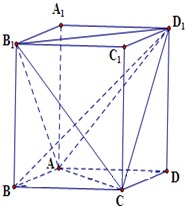 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AB=1,AA1=
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AB=1,AA1=