题目内容
观察下列等式:
(1+1)=2×1
(2+1)(2+2)=22×1×3
(3+1)(3+2)(3+3)=23×1×3×5
…
照以上式子规律:
(1)写出第4个等式,并猜想第n个等式;(n∈N*)
(2)用数学归纳法证明上述所猜想的第n个等式成立.(n∈N*)
(1+1)=2×1
(2+1)(2+2)=22×1×3
(3+1)(3+2)(3+3)=23×1×3×5
…
照以上式子规律:
(1)写出第4个等式,并猜想第n个等式;(n∈N*)
(2)用数学归纳法证明上述所猜想的第n个等式成立.(n∈N*)
考点:数学归纳法,归纳推理
专题:点列、递归数列与数学归纳法
分析:(1)利用已知条件,观察规律写出第4个等式,并猜想第n个等式;(n∈N*)
(2)用数学归纳法的证明步骤证明上述所猜想的第n个等式成立.(n∈N*)
(2)用数学归纳法的证明步骤证明上述所猜想的第n个等式成立.(n∈N*)
解答:
解:(1)(1+1)=2×1,
(2+1)(2+2)=22×1×3,
(3+1)(3+2)(3+3)=23×1×3×5,
第4个等式,(4+1)(4+2)(4+3)(4+4)=24×1×3×5×7;
猜想第n个等式:(n+1)(n+2)(n+3)…(n+n)=2n×1×3×5×…×(2n-1)(n∈N*)
(2)①当n=1时,左边=(1+1)=2,右边=2×1=2等式成立;
②假设当n=k时,原式成立,即:(k+1)(k+2)(k+3)…(k+k)=2k×1×3×5×…×(2k-1)(k∈N*)
那么,当n=k+1时,左边=:(k+1+1)(k+1+2)(k+1+3)…(k+1+k-1)(k+1+k)(k+1+k+1)
=
=
=2k+1×1×3×5×…×(2k+1)=右边,
故n=k+1时,等式也成立.
由①②知:(n+1)(n+2)(n+3)…(n+n)=2n×1×3×5×…×(2n-1)(n∈N*) 成立.
(2+1)(2+2)=22×1×3,
(3+1)(3+2)(3+3)=23×1×3×5,
第4个等式,(4+1)(4+2)(4+3)(4+4)=24×1×3×5×7;
猜想第n个等式:(n+1)(n+2)(n+3)…(n+n)=2n×1×3×5×…×(2n-1)(n∈N*)
(2)①当n=1时,左边=(1+1)=2,右边=2×1=2等式成立;
②假设当n=k时,原式成立,即:(k+1)(k+2)(k+3)…(k+k)=2k×1×3×5×…×(2k-1)(k∈N*)
那么,当n=k+1时,左边=:(k+1+1)(k+1+2)(k+1+3)…(k+1+k-1)(k+1+k)(k+1+k+1)
=
| [(k+1)(k+2)(k+3)…(k+1+k-1)](k+1+k)(k+1+k+1) |
| k+1 |
=
| 2k×1×3×5×…×(2k-1)(2k+1)(2k+2) |
| k+1 |
=2k+1×1×3×5×…×(2k+1)=右边,
故n=k+1时,等式也成立.
由①②知:(n+1)(n+2)(n+3)…(n+n)=2n×1×3×5×…×(2n-1)(n∈N*) 成立.
点评:本题考查数学归纳法证明猜想成立,注意证明步骤的应用,缺一不可.

练习册系列答案
相关题目
 空间四边形ABCD的每条边和对角线的长都等于a,点M、N分别是边AB、CD的中点,求证:
空间四边形ABCD的每条边和对角线的长都等于a,点M、N分别是边AB、CD的中点,求证: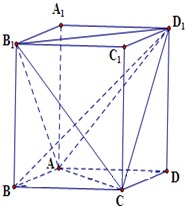 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AB=1,AA1=
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AB=1,AA1=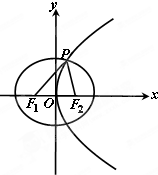 已知离心率为
已知离心率为
