题目内容

已知f（x）满足f（x+2）=f（x），且当0≤x＜2时，f（x）=x3-x，则函数y=f（x）的图象在区间[0，6]上与x轴的交点的个数为（　　）
A、6B、7C、8D、9
考点：函数的零点与方程根的关系
专题：函数的性质及应用
分析：由条件可得可得函数的周期为2，由于当0≤x＜2时，f（x）=x3-x=x（x+1）（x-1）的零点有2个，可得函数在区间[0，6]上的零点个数为6，从而得出结论．
解答： 解：由f（x+2）=f（x），可得函数的周期为2．
由于当0≤x＜2时，f（x）=x3-x=x（x+1）（x-1），
故函数在一个周期[0，2）上的零点有2个：x=0 x=1
故函数在区间[0，6]上的零点个数为6．
由于函数y=f（x）的图象在区间[0，6]上与x轴的交点的个数，即函数在区间[0，6]上的零点个数，
故选：A．
点评：本题主要考查函数的零点的定义，利用函数的周期性求函数的零点个数，体现了转化的数学思想，属于基础题．
练习册系列答案
相关题目
给出下列命题：
①终边相同的角的同名函数值相等；
②终边不同的角的同名函数值不相等；
③若sinα＞0，则α是第一或第二象限的角；
④若α是第二象限角，且P（x，y）是其终边上的一点，则cosα=
-x
x2+y2
；
⑤若α、β是第二象限的角，且α＞β，则cosα＜cosβ．
其中正确的命题有（　　）
A、1个B、2个C、3个D、4个
下列命题正确的个数是（　　）
（1）若直线l上有无数个点不在α内，则l∥α
（2）若直线l与平面α平行，l与平面α内的任意一直线平行
（3）两条平行线中的一条直线与平面平行，那么另一条也与这个平面平行
（4）若一直线a和平面α内一直线b平行，则a∥α
A、0个B、1个C、2个D、3个
阅读如图程序：如果输入5，则该程序运行结果为（　　）
A、1B、10C、25D、26
等差数列{an}中，a3+a7=15，则a2+a8=（　　）
A、10B、15C、12D、8
已知向量
a
=（cos3φ，sin3φ），
b
=（cos（α-φ），sin（α-φ）），φ∈[0，
π
4
]，
b
=x
a
（x＞0）．
（1）求|
a
|的取值范围；
（2）设
3
cosα=y，求y与x的函数关系式y=f（x），并指出其定义域；
（3）设正项数列{an}满足a1=1，an+1=f（an），求数列{an}的通项公式．
空间四边形ABCD的每条边和对角线的长都等于a，点M、N分别是边AB、CD的中点，求证：
（1）MN为AB和CD的公垂线；     
（2）求MN的长；
（3）求异面直线AN与CM所成角的余弦值．
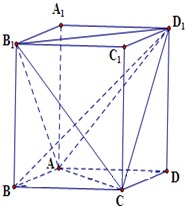如图，直四棱柱ABCD-A1B1C1D1的底面ABCD为菱形，AB=1，AA1=
6
2
，∠ABC=60°．证明：BD1⊥平面AB1C．
设函数f（x）=2sin（2ωx-
π
6
）+λ（x∈R）的图象关于直线x=π对称，其中ω，λ为常数，且ω∈（
1
2
，1）
（1）求函数f（x）的最小正周期；
（2）若y=f（x）的图象经过点（
π
4
，0），求函数f（x）的值域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网