题目内容
已知函数f(x)=ex+e-x,其中e是自然对数的底数.
(1)证明:f(x)是R上的偶函数;
(2)若关于x的不等式mf(x)≤e-x+m-1在(0,+∞)上恒成立,求实数m的取值范围.
(1)证明:f(x)是R上的偶函数;
(2)若关于x的不等式mf(x)≤e-x+m-1在(0,+∞)上恒成立,求实数m的取值范围.
考点:函数恒成立问题
专题:综合题,函数的性质及应用
分析:(1)根据函数奇偶性的定义即可证明f(x)是R上的偶函数;
(2)利用参数分离法,将不等式mf(x)≤e-x+m-1在(0,+∞)上恒成立,进行转化求最值问题即可求实数m的取值范围.
(2)利用参数分离法,将不等式mf(x)≤e-x+m-1在(0,+∞)上恒成立,进行转化求最值问题即可求实数m的取值范围.
解答:
(1)证明:∵f(x)=ex+e-x,
∴f(-x)=e-x+ex=f(x),即函数:f(x)是R上的偶函数;
(2)解:若关于x的不等式mf(x)≤e-x+m-1在(0,+∞)上恒成立,
即m(ex+e-x-1)≤e-x-1,
∵x>0,
∴ex+e-x-1>0,
即m≤
在(0,+∞)上恒成立,
设t=ex,(t>1),则m≤
在(1,+∞)上恒成立,
∵
=-
=-
≥-
,当且仅当t=2时等号成立,
∴m≤-
.
∴f(-x)=e-x+ex=f(x),即函数:f(x)是R上的偶函数;
(2)解:若关于x的不等式mf(x)≤e-x+m-1在(0,+∞)上恒成立,
即m(ex+e-x-1)≤e-x-1,
∵x>0,
∴ex+e-x-1>0,
即m≤
| e-x-1 |
| ex+e-x-1 |
设t=ex,(t>1),则m≤
| 1-t |
| t2-t+1 |
∵
| 1-t |
| t2-t+1 |
| t-1 |
| (t-1)2+(t-1)+1 |
| 1 | ||
t-1+
|
| 1 |
| 3 |
∴m≤-
| 1 |
| 3 |
点评:本题主要考查函数奇偶性的判定,函数单调性和最值的应用,属于中档题.

练习册系列答案
相关题目
等差数列{an}中,a3+a7=15,则a2+a8=( )
| A、10 | B、15 | C、12 | D、8 |
 已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段B1B,AB和A1C上的动点,观察直线CE与D1F,CE与D1G.给出下列结论:
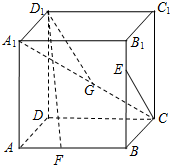
已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段B1B,AB和A1C上的动点,观察直线CE与D1F,CE与D1G.给出下列结论: 空间四边形ABCD的每条边和对角线的长都等于a,点M、N分别是边AB、CD的中点,求证:
空间四边形ABCD的每条边和对角线的长都等于a,点M、N分别是边AB、CD的中点,求证: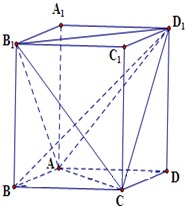 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AB=1,AA1=
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AB=1,AA1=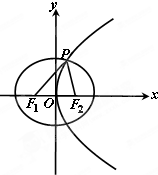 已知离心率为
已知离心率为