题目内容

当n为正整数时，试比较2n与n2的大小，并给出必要的证明过程．
考点：不等式比较大小
专题：不等式的解法及应用
分析：当n=1时，21＞12；当n=2时，22=22；当n=3时，23＜32；当n=4时，24=42；当n≥5时，2n＞n2．利用二项式定理即可得出．
解答： 解：当n=1时，21＞12；
当n=2时，22=22；
当n=3时，23＜32；
当n=4时，24=42；
当n≥5时，2n＞n2．
∵2n=（1+1）n=1+
C
1
n
+
C
2
n
+
C
3
n
+…＞2(1+
C
1
n
+
C
2
n
)=2+2n+n（n-1）=n2+n+2＞n2．
点评：本题考查了二项式定理的应用、指数函数和幂函数的性质，考查了分类讨论的思想方法，属于中档题．
练习册系列答案
相关题目
阅读如图程序：如果输入5，则该程序运行结果为（　　）
A、1B、10C、25D、26
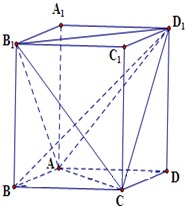如图，直四棱柱ABCD-A1B1C1D1的底面ABCD为菱形，AB=1，AA1=
6
2
，∠ABC=60°．证明：BD1⊥平面AB1C．
已知函数f（x）=
ex
ex
，g（x）=mx-lnx-tm．
（1）求函数f（x）在x∈（0，+∞）上的值域；
（2）若m∈[
e
，e2]，对?x1，x2∈（0，+∞），f（x1）≤g（x2）恒成立，求实数t的取值范围．
化简：(
1
2
)2+(
1
2
)4+(
1
2
)6+…+(
1
2
)n-1（n为奇数）．
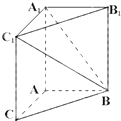如图，在三棱柱ABC-A1B1C1中，AA1C1C是边长为4的正方形，平面ABC⊥平面AA1C1C，AB=3，BC=5．
（1）求证：AA1⊥平面ABC；
（2）求点A1到平面B1BCC1的距离；
（3）求二面角A1-BC1-B1的正弦值．
设函数f（x）=2sin（2ωx-
π
6
）+λ（x∈R）的图象关于直线x=π对称，其中ω，λ为常数，且ω∈（
1
2
，1）
（1）求函数f（x）的最小正周期；
（2）若y=f（x）的图象经过点（
π
4
，0），求函数f（x）的值域．
某货轮匀速行驶在相距300海里的甲、乙两地间，运输成本由燃料费用和其它费用组成，已知该货轮每小时的燃料费用与其航行速度的平方成正比（比例系数为0.5），其它费用为每小时m元，根据市场调研，得知m的波动区间是[1000，1600]，且该货轮的最大航行速度为50海里/小时．
（1）请将从甲地到乙地的运输成本y（元）表示为航行速度x（海里/小时）的函数；
（2）要使从甲地到乙地的运输成本最少，该货轮应以多大的航行速度行驶？
正项数列{an}满足a1=1，a2=2，又数列{
anan+1
}是以
2
2
为公比的等比数列，则使得不等式
1
a1
+
1
a2
+…+
1
a2n+1
＜1280成立的最大整数n为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网