题目内容
已知函数f(x)=
x3+ax2-4在区间(0,2)上是减函数,则a的范围是( )
| 1 |
| 3 |
| A、(-∞,3] |
| B、[-1,+∞) |
| C、[3,+∞) |
| D、(-∞,-1] |
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:先求出函数的导数,由题意得不等式,解出即可.
解答:
解:∵f′(x)=x2+2ax,
∴f′(2)=4+4a≤0,
解得:a≤-1,
故选;D.
∴f′(2)=4+4a≤0,
解得:a≤-1,
故选;D.
点评:本题考察了函数的单调性,导数的应用,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
给出下列命题:
①终边相同的角的同名函数值相等;
②终边不同的角的同名函数值不相等;
③若sinα>0,则α是第一或第二象限的角;
④若α是第二象限角,且P(x,y)是其终边上的一点,则cosα=
;
⑤若α、β是第二象限的角,且α>β,则cosα<cosβ.
其中正确的命题有( )
①终边相同的角的同名函数值相等;
②终边不同的角的同名函数值不相等;
③若sinα>0,则α是第一或第二象限的角;
④若α是第二象限角,且P(x,y)是其终边上的一点,则cosα=
| -x | ||
|
⑤若α、β是第二象限的角,且α>β,则cosα<cosβ.
其中正确的命题有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
若a=21.2,b=(
)-0.8,c=2log52,则( )
| 1 |
| 2 |
| A、c<b<a |
| B、b<a<c |
| C、c<a<b |
| D、b<c<a |
下列函数在(1,+∞)上是增函数的是( )
| A、y=-2x | ||
B、y=log
| ||
| C、y=-(x-1) | ||
| D、y=|x-1| |
下列命题正确的个数是( )
(1)若直线l上有无数个点不在α内,则l∥α
(2)若直线l与平面α平行,l与平面α内的任意一直线平行
(3)两条平行线中的一条直线与平面平行,那么另一条也与这个平面平行
(4)若一直线a和平面α内一直线b平行,则a∥α
(1)若直线l上有无数个点不在α内,则l∥α
(2)若直线l与平面α平行,l与平面α内的任意一直线平行
(3)两条平行线中的一条直线与平面平行,那么另一条也与这个平面平行
(4)若一直线a和平面α内一直线b平行,则a∥α
| A、0个 | B、1个 | C、2个 | D、3个 |
阅读如图程序:如果输入5,则该程序运行结果为( )


| A、1 | B、10 | C、25 | D、26 |
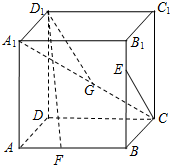 已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段B1B,AB和A1C上的动点,观察直线CE与D1F,CE与D1G.给出下列结论:
已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段B1B,AB和A1C上的动点,观察直线CE与D1F,CE与D1G.给出下列结论: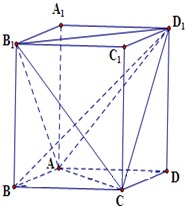 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AB=1,AA1=
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AB=1,AA1=