题目内容
力综合治理交通拥堵状况,缓解机动车过快增长势头,一些大城市出台了“机动车摇号上牌”的新规.某大城市2014年初机动车的保有量为600万辆,预计此后每年将报废本年度机动车保有量的5%,且报废后机动车的牌照不再使用,同时每年投放10万辆的机动车牌号,只有摇号获得指标的机动车才能上牌,经调研,获得摇号指标的市民通常都会在当年购买机动车上牌.
(Ⅰ)问:到2018年初,该城市的机动车保有量为多少万辆;
(Ⅱ)根据该城市交通建设规划要求,预计机动车的保有量少于500万辆时,该城市交通拥堵状况才真正得到缓解.问:至少需要多少年可以实现这一目标.(参考数据:0.954=0.81,0.955=0.77,lg0.75=-0.13,lg0.95=-0.02)
(Ⅰ)问:到2018年初,该城市的机动车保有量为多少万辆;
(Ⅱ)根据该城市交通建设规划要求,预计机动车的保有量少于500万辆时,该城市交通拥堵状况才真正得到缓解.问:至少需要多少年可以实现这一目标.(参考数据:0.954=0.81,0.955=0.77,lg0.75=-0.13,lg0.95=-0.02)
考点:数列与函数的综合
专题:等差数列与等比数列
分析:(Ⅰ)设2012年年初机动车保有量为a1万辆,由已知条件推导出数列{an-200}是以400为首项,0.95为公比的等比数列,由此能求出2016年初机动车保有量.
(Ⅱ)由题意知,an=400•0.95n-1+200<500,由此能求出至少需要8年时间才能实现目标.
(Ⅱ)由题意知,an=400•0.95n-1+200<500,由此能求出至少需要8年时间才能实现目标.
解答:
解:(Ⅰ)设2012年年初机动车保有量为a1万辆,
以后各年年初机动车保有量依次为a2万辆,a3万辆,…,每年新增机动车10万辆,
则a1=600,an+1=0.95a1+10,
又an+1-200=0.95(an-200),
且a1-200=600-200=400,
∴数列{an-200}是以400为首项,0.95为公比的等比数列,
∴an-200=400•0.95n-1,即an=400•0.95n-1+200,
∴2018年初机动车保有量为a5=400•0.954+200=524万辆.
(Ⅱ)由题意知,an=400•0.95n-1+200<500,
即0.95n-1<0.75,
∴n>
+1=7.5.
故至少需要8年时间才能实现目标.
以后各年年初机动车保有量依次为a2万辆,a3万辆,…,每年新增机动车10万辆,
则a1=600,an+1=0.95a1+10,
又an+1-200=0.95(an-200),
且a1-200=600-200=400,
∴数列{an-200}是以400为首项,0.95为公比的等比数列,
∴an-200=400•0.95n-1,即an=400•0.95n-1+200,
∴2018年初机动车保有量为a5=400•0.954+200=524万辆.
(Ⅱ)由题意知,an=400•0.95n-1+200<500,
即0.95n-1<0.75,
∴n>
| lg0.75 |
| lg0.95 |
故至少需要8年时间才能实现目标.
点评:本题考查数列与函数的综合运用,是中档题,解题时要认真审题,注意等比数列的性质的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在极坐标系中,曲线ρ(cosθ+sinθ)=1,则曲线在直角坐标系中方程为( )
| A、x+y=2 | B、x-y=1 |
| C、x=1 | D、x+y=1 |
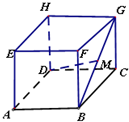 如图,正方体ABCD-EFGH中,M为BG的中点,则直线DM与平面ABCD所成角的正切值为( )
如图,正方体ABCD-EFGH中,M为BG的中点,则直线DM与平面ABCD所成角的正切值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
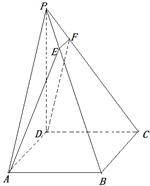 如图,已知ABCD是正方形,PD⊥平面ABCD,
如图,已知ABCD是正方形,PD⊥平面ABCD,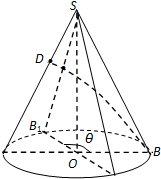 如图已知圆锥SO的底面半径为4,母线长为8,三角形SAB是圆锥的一个轴截面,D是SA上的一点,且
如图已知圆锥SO的底面半径为4,母线长为8,三角形SAB是圆锥的一个轴截面,D是SA上的一点,且