题目内容
已知f(x)=
,若对任意x∈[-1-m,m-1],不等式f(
x-m)≥[f(x)]3恒成立,求实数m的取值范围.
|
| 2 |
考点:函数最值的应用
专题:计算题,函数的性质及应用
分析:分段函数内都是指数函数,且底数都大于1,借助指数运算及单调性化简不等式,同时注意区间成立的条件从而求出实数m的取值范围.
解答:
解:有题设知,f(x)=
,则[f(x)]3=f(3x),
因此原不等式等价于f(
x-m)≥f(3x),
又∵f(x)在R上是增函数,
∴
x-m≥3x,
即m≤(
-3)x,且x∈[-1-m,m-1],
∴当x=m-1时,(
-3)x取得最小值(
-3)(m-1),
因此m≤(
-3)(m-1),
解得m≤
,
又∵m-1>-1-m,
∴m>0,
故m∈(0,
].
|
因此原不等式等价于f(
| 2 |
又∵f(x)在R上是增函数,
∴
| 2 |
即m≤(
| 2 |
∴当x=m-1时,(
| 2 |
| 2 |
因此m≤(
| 2 |
解得m≤
2-
| ||
| 2 |
又∵m-1>-1-m,
∴m>0,
故m∈(0,
2-
| ||
| 2 |
点评:本题综合考查了学生对分段函数,指数函数,指数运算及不等式的处理能力.将题目条件转化为常见题型的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
曲线x2+y2+4x-4y=0关于( )
| A、直线x=4对称 |
| B、直线x+y=0对称 |
| C、直线x-y=0对称 |
| D、直线(-4,4)对称 |
已知双曲线
-
=1的一条渐近线方程为4x+3y=0,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示是《函数的应用》的知识结构图,如果要加入“用二分法求方程的近似解”,则应该放在( )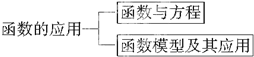

| A、“函数与方程”的上位 |
| B、“函数与方程”的下位 |
| C、“函数模型及其应用”的上位 |
| D、“函数模型及其应用”的下位 |
 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=4,AD=2,PA=2,PD=
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=4,AD=2,PA=2,PD=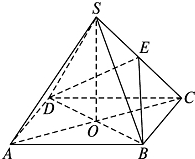 如图,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,O是AC与BD的交点,SO⊥平面ABCD,E是侧棱SC的中点,直线SA和AO所成角的大小是45°.
如图,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,O是AC与BD的交点,SO⊥平面ABCD,E是侧棱SC的中点,直线SA和AO所成角的大小是45°.