题目内容
在极坐标系中，曲线ρ（cosθ+sinθ）=1，则曲线在直角坐标系中方程为（ ）
| A、x+y=2 | B、x-y=1 |
| C、x=1 | D、x+y=1 |
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：运用x=ρcosθ，y=ρsinθ，代入即可．
解答：
解：将x=ρcosθ，y=ρsinθ，
代入曲线ρ（cosθ+sinθ）=1，
得x+y=1．
故选D．
代入曲线ρ（cosθ+sinθ）=1，
得x+y=1．
故选D．
点评：本题主要考查极坐标与直角坐标的关系式：x=ρcosθ，y=ρsinθ，是一道基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知f（x）=xln x，若f′（x0）=2，则x0等于（ ）
| A、e2 | ||
| B、e | ||
C、
| ||
| D、ln 2 |
函数y=cosx•ln|x|的部分图象大致是下图中的（ ）
A、 |
B、 |
C、 |
D、 |
三次函数f（x）=ax3+2x+5在x∈（-∞，+∞）内是增函数，则（ ）
| A、a＞0 | ||
| B、a＜0 | ||
| C、a=1 | ||
D、a=
|
曲线x2+y2+4x-4y=0关于（ ）
| A、直线x=4对称 |
| B、直线x+y=0对称 |
| C、直线x-y=0对称 |
| D、直线（-4，4）对称 |
已知a是2和6的等差中项，则a为（ ）
A、2
| ||
B、
| ||
| C、4 | ||
| D、3 |
把函数y=cosx的图象向左平移
个单位，然后把，图象上的所有点的横坐标缩小到原来的
（纵坐标不变），则所得图形对应的函数解析式为（ ）
| π |
| 4 |
| 1 |
| 2 |
A、y=cos（
| ||||
B、y=cos（2x+
| ||||
C、y=cos（
| ||||
D、y=cos（2x+
|
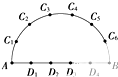如图，在以AB为直径的半圆周上，有异于A、B的六个点C1、C2、C3、C4、C5、C6，直径AB上有异于A、B的四个点D1、D2、D3、D4．以这10个点中的3个点为顶点作三角形可作出多少个（ ）