题目内容
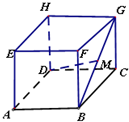 如图,正方体ABCD-EFGH中,M为BG的中点,则直线DM与平面ABCD所成角的正切值为( )
如图,正方体ABCD-EFGH中,M为BG的中点,则直线DM与平面ABCD所成角的正切值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:直线与平面所成的角
专题:空间角
分析:过M作MN⊥BC,交BC于N,连结DN,则∠MDN直线DM与平面ABCD所成角,由此能求出直线与平面所成角的正切值.
解答:
解: 过M作MN⊥BC,交BC于N,连结DN,
过M作MN⊥BC,交BC于N,连结DN,
∵正方体ABCD-EFGH中,M为BG的中点,
∴MN⊥平面ABCD,
∴∠MDN直线DM与平面ABCD所成角,
设正方体ABCD-EFGH的棱长为a,
则MN=
a,DN=
=
a,
∴tan∠MDN=
=
=
.
故选:B.
 过M作MN⊥BC,交BC于N,连结DN,
过M作MN⊥BC,交BC于N,连结DN,∵正方体ABCD-EFGH中,M为BG的中点,
∴MN⊥平面ABCD,
∴∠MDN直线DM与平面ABCD所成角,
设正方体ABCD-EFGH的棱长为a,
则MN=
| 1 |
| 2 |
a2+(
|
| ||
| 2 |
∴tan∠MDN=
| MN |
| DN |
| ||||
|
| ||
| 5 |
故选:B.
点评:本题考查直线与平面所成角的正切值的求法,解题时要认真审题,注意空间思维能力的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=cosx•ln|x|的部分图象大致是下图中的( )
A、 |
B、 |
C、 |
D、 |
把函数y=cosx的图象向左平移
个单位,然后把,图象上的所有点的横坐标缩小到原来的
(纵坐标不变),则所得图形对应的函数解析式为( )
| π |
| 4 |
| 1 |
| 2 |
A、y=cos(
| ||||
B、y=cos(2x+
| ||||
C、y=cos(
| ||||
D、y=cos(2x+
|
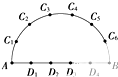 如图,在以AB为直径的半圆周上,有异于A、B的六个点C1、C2、C3、C4、C5、C6,直径AB上有异于A、B的四个点D1、D2、D3、D4.以这10个点中的3个点为顶点作三角形可作出多少个( )
如图,在以AB为直径的半圆周上,有异于A、B的六个点C1、C2、C3、C4、C5、C6,直径AB上有异于A、B的四个点D1、D2、D3、D4.以这10个点中的3个点为顶点作三角形可作出多少个( )| A、116 | B、128 |
| C、215 | D、98 |
已知双曲线
-
=1的一条渐近线方程为4x+3y=0,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
现有数列{an}满足:a1=1,且对任意的m,n∈N*都有:am+n=am+an+mn,则
+
+
+…+
=
( )
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a2014 |
( )
A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示是《函数的应用》的知识结构图,如果要加入“用二分法求方程的近似解”,则应该放在( )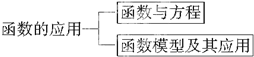

| A、“函数与方程”的上位 |
| B、“函数与方程”的下位 |
| C、“函数模型及其应用”的上位 |
| D、“函数模型及其应用”的下位 |
 如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.
如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.