题目内容
已知圆C:x2+y2-2ax+2=0与直线y=x相切,则a= .
考点:利用导数研究曲线上某点切线方程
专题:计算题,直线与圆
分析:由直线与圆相切,得到圆心到直线的距离等于圆的半径,利用点到直线的距离公式列出关于a的方程,求出方程的解即可得到a的值.
解答:
解:圆C:x2+y2-2ax+2=0,可化为(x-a)2+y2=a2-2,
∴圆心为(a,0),半径为
,
∵圆C:x2+y2-2ax+2=0与直线y=x相切,
∴
=
,
∴a=±2.
故答案为:±2.
∴圆心为(a,0),半径为
| a2-2 |
∵圆C:x2+y2-2ax+2=0与直线y=x相切,
∴
| |a| | ||
|
| a2-2 |
∴a=±2.
故答案为:±2.
点评:此题考查了直线与圆的位置关系,当直线与圆相切时,圆心到直线的距离等于圆的半径,熟练掌握此性质是解本题的关键.

练习册系列答案
相关题目
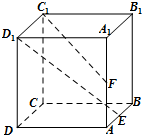 已知点E、F分别是正方体ABCD-A1B1C1D1的棱AB、AA1的中点,点M、N分别是线段D1E与C1F上的点,则满足与平面ABCD平行的直线MN有( )
已知点E、F分别是正方体ABCD-A1B1C1D1的棱AB、AA1的中点,点M、N分别是线段D1E与C1F上的点,则满足与平面ABCD平行的直线MN有( )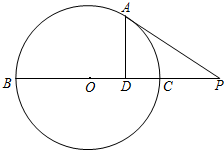 如图所示,PA与圆O相切于A,直线PO交圆O于B,C两点,AD⊥BC,垂足为D,且D是OC的中点,若PA=6,则PC=
如图所示,PA与圆O相切于A,直线PO交圆O于B,C两点,AD⊥BC,垂足为D,且D是OC的中点,若PA=6,则PC=