题目内容
设等差数列{an}的前n项和为Sn,且S4=4S2,a4=2a2+1,求数列{an}的通项公式及前n项和Sn.
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:根据等差数列的通项公式,建立方程即可得到公差d和首项,即可得到结论.
解答:
解:由等差数列的前n项和公式可得
,
即
,
解得a1=1,d=2,
即an=1+2(n-1)=2n-1,Sn=n+
×2=n2.
|
即
|
解得a1=1,d=2,
即an=1+2(n-1)=2n-1,Sn=n+
| n(n-1) |
| 2 |
点评:本题主要考查等差数列的通项公式和前n项和的计算,建立方程组是解决本题的关键.

练习册系列答案
相关题目
已知cosα=
,α是第四象限角,则sinα=( )
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|

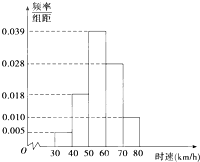 经过随机抽样获得100辆汽车经过某一雷达测速地区的时速(单位:km/h),并绘制成如图所示的频率分布直方图,其中这100辆汽车时速的范围是[30,80],数据分组为[30,40),[40,50),[50,60),[60,70),[70,80].设时速达到或超过60km/h的汽车有x辆,则x等于
经过随机抽样获得100辆汽车经过某一雷达测速地区的时速(单位:km/h),并绘制成如图所示的频率分布直方图,其中这100辆汽车时速的范围是[30,80],数据分组为[30,40),[40,50),[50,60),[60,70),[70,80].设时速达到或超过60km/h的汽车有x辆,则x等于