题目内容
函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则下列正确的是( )
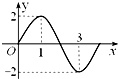

A、y=2sin
| ||
| B、y=2sinπx | ||
C、y=sin
| ||
| D、y=2sin2x |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,从而得到函数的解析式.
解答:
解:由函数的图象的顶点坐标可得A=2,再根据
T=
•
=3-1,可得ω=
.
由函数的图象过原点可得φ=0,故函数的解析式为y=2sin
x,
故选:A.
| 1 |
| 2 |
| 1 |
| 2 |
| 2π |
| ω |
| π |
| 2 |
由函数的图象过原点可得φ=0,故函数的解析式为y=2sin
| π |
| 2 |
故选:A.
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,属于基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
在△ABC中,若sin(A+B+C)=sin(A-B+C),则△ABC的形状一定是( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰或直角三角形 |
| D、等腰直角三角形 |
已知a,b为不相等的两正数,且a3-b3=a2-b2,则a+b的取值范围是( )
A、(0,
| ||
B、(1,
| ||
C、(
| ||
| D、(1,2) |
某单位有若干部门,现召开一个70人的座谈会,决定用分层抽样的方法从各部门选取代表,其中一个部门20人中被抽取4人,则这个单位应有( )
| A、200人 | B、250人 |
| C、300人 | D、350人 |
设甲、乙两楼相距20m,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则甲、乙两楼的高分别是( )
A、20
| ||||||||
B、10
| ||||||||
C、10(
| ||||||||
D、
|
给定数列,1,2+3+4,5+6+7+8+9,10+11+12+13+14+15+16,…则这个数列的通项公式是( )
| A、an=2n2+3n-1 |
| B、an=n2+5n-5 |
| C、an=2n3-3n2+3n-1 |
| D、an=2n3-n2+n-2 |
已知
1,
2是一对不共线向量,若
=
1+λ
2,
=-2λ
1-
2且
,
共线,则λ的值为( )
| e |
| e |
| a |
| e |
| e |
| b |
| e |
| e |
| a |
| b |
A、±
| ||||
B、±
| ||||
C、
| ||||
D、-
|