题目内容
已知a,b为不相等的两正数,且a3-b3=a2-b2,则a+b的取值范围是( )
A、(0,
| ||
B、(1,
| ||
C、(
| ||
| D、(1,2) |
考点:基本不等式
专题:不等式的解法及应用
分析:根据题意及立方差公式的展开形式可得出a2+ab+b2=a+b的值,然后可求出ab与a+b的关系式,结合基本不等式即可得出答案.
解答:
解:∵a3-b3=a2-b2,
∴(a-b)(a2+ab+b2)=(a-b)(a+b)
∵a,b为不相等的两正数
∴a2+ab+b2=a+b,
∴(a+b)2-(a+b)=ab,
又0< ab<
∴0<(a+b)2-(a+b)<
,
解得,1<a+b<
,
故选:B.
∴(a-b)(a2+ab+b2)=(a-b)(a+b)
∵a,b为不相等的两正数
∴a2+ab+b2=a+b,
∴(a+b)2-(a+b)=ab,
又0< ab<
| (a+b)2 |
| 4 |
∴0<(a+b)2-(a+b)<
| (a+b)2 |
| 4 |
解得,1<a+b<
| 4 |
| 3 |
故选:B.
点评:本题考查基本不等式、立方公式的应用,难度不大,注意掌握立方公式的特点结合完全平方式是解答本题的关键.

练习册系列答案
相关题目
已知复数z=-
+
i,则
=( )
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| z |
A、-
| ||||||
B、-
| ||||||
C、
| ||||||
D、
|
设α,β是两个不同的平面,l是一条直线,以下命题:①若l⊥α,α⊥β,则l?β,②若l∥α,α∥β,则l?β③若l⊥α,α∥β,则l⊥β,④若l∥α,α⊥β,则l⊥β 其中正确命题的个数是( )
| A、1 | B、2 | C、3 | D、0 |
设△ABC的面积为S,已知S=a2-(b-c)2,则tan
的值为( )
| A |
| 2 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
函数f(x)=ax3+x恰有三个单调区间,则a的取值范围是( )
A、(-∞,-
| ||
B、[-
| ||
| C、[0,+∞) | ||
| D、(-∞,0) |
函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则下列正确的是( )
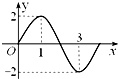

A、y=2sin
| ||
| B、y=2sinπx | ||
C、y=sin
| ||
| D、y=2sin2x |
等差数列{an}的前n项和Sn满足:S13=2184,则3(a3+a5)+2(a7+a10+a13)的值是( )
| A、2013 | B、2016 |
| C、2014 | D、不确定 |
已知双曲线
-
=1,(a>b>0),两渐近线的夹角为
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、2或
|