题目内容
设甲、乙两楼相距20m，从乙楼底望甲楼顶的仰角为60°，从甲楼顶望乙楼顶的俯角为30°，则甲、乙两楼的高分别是（ ）
A、20
| ||||||||
B、10
| ||||||||
C、10（
| ||||||||
D、
|
考点：余弦定理,正弦定理
专题：三角函数的求值
分析：根据题意画出图形，如图所示，在三角形ABD中，由BD与∠ABD度数，利用锐角三角函数定义求出AD与AB的长，确定出甲楼高；在三角形ABC中，利用余弦定理列出关系式，将AB与cos∠ACB的值代入求出BC的长，即为乙楼高．
解答：
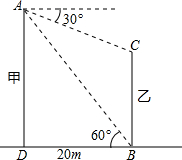解：如图所示，
在Rt△ABD中，∠ABD=60°，BD=20m，
∴AD=BDtan60°=20
m，AB=
=40m，
∵∠CAB=∠ABC=30°，
∴AC=BC，∠ACB=120°，
在△ABC中，设AC=BC=x，
由余弦定理得：AB2=AC2+BC2-2AC•BC•cos∠ACB，即1600=x2+x2+x2，
解得：x=
，
则甲、乙两楼的高分别是20
m，
m．
故选：A．
解：如图所示，在Rt△ABD中，∠ABD=60°，BD=20m，
∴AD=BDtan60°=20
| 3 |
| 20 |
| cos60° |
∵∠CAB=∠ABC=30°，
∴AC=BC，∠ACB=120°，
在△ABC中，设AC=BC=x，
由余弦定理得：AB2=AC2+BC2-2AC•BC•cos∠ACB，即1600=x2+x2+x2，
解得：x=
| 40 |
| 3 |
| 3 |
则甲、乙两楼的高分别是20
| 3 |
| 40 |
| 3 |
| 3 |
故选：A．
点评：此题考查了余弦定理，锐角三角函数定义，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
设α，β是两个不同的平面，l是一条直线，以下命题：①若l⊥α，α⊥β，则l?β，②若l∥α，α∥β，则l?β③若l⊥α，α∥β，则l⊥β，④若l∥α，α⊥β，则l⊥β 其中正确命题的个数是（ ）
| A、1 | B、2 | C、3 | D、0 |
函数f（x）=ax3+x恰有三个单调区间，则a的取值范围是（ ）
A、（-∞，-
| ||
B、[-
| ||
| C、[0，+∞） | ||
| D、（-∞，0） |
函数y=Asin（ωx+φ）（A＞0，ω＞0）的部分图象如图所示，则下列正确的是（ ）
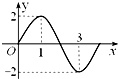
A、y=2sin
| ||
| B、y=2sinπx | ||
C、y=sin
| ||
| D、y=2sin2x |
函数f（x）=
在[-2，2]上的最大值为1，则实数a的取值范围是（ ）
|
| A、[0，+∞） |
| B、[0，e] |
| C、（-∞，0] |
| D、（-∞，e] |
等差数列{an}的前n项和Sn满足：S13=2184，则3（a3+a5）+2（a7+a10+a13）的值是（ ）
| A、2013 | B、2016 |
| C、2014 | D、不确定 |
下列求导运算错误的是（ ）
| A、x′=1 | ||
B、（log2x）′=
| ||
| C、（ex）′=ex | ||
| D、（sinx）′=cosx |