题目内容
在△ABC中，若sin（A+B+C）=sin（A-B+C），则△ABC的形状一定是（ ）
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰或直角三角形 |
| D、等腰直角三角形 |
考点：两角和与差的正弦函数
专题：解三角形
分析：由题意可得0=sin（A-B+C），A-B+C=0，即B=A+C=
，可得△ABC的形状一定是直角三角形．
| π |
| 2 |
解答：
解：△ABC中，若sin（A+B+C）=sinπ=0=sin（A-B+C），
∴A-B+C=0，∴B=A+C=
，∴△ABC的形状一定是直角三角形，
故选：B．
∴A-B+C=0，∴B=A+C=
| π |
| 2 |
故选：B．
点评：本题主要考查两角和的正弦公式，判断三角形的形状，属于基础题．
练习册系列答案
相关题目
在一个盒子中有分别标有数字0，1，2，3，4的5张卡片，现从中一次取出2张卡片，则取到的卡片上的数字之和为偶数的概率是已知复数z=-
+
i，则
=（ ）
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| z |
A、-
| ||||||
B、-
| ||||||
C、
| ||||||
D、
|
（文科）在△ABC中，如果sinA：sinB：sinC=2：3：4，那么最大角的余弦值等于（ ）
A、
| ||
B、-
| ||
C、-
| ||
D、-
|
设α，β是两个不同的平面，l是一条直线，以下命题：①若l⊥α，α⊥β，则l?β，②若l∥α，α∥β，则l?β③若l⊥α，α∥β，则l⊥β，④若l∥α，α⊥β，则l⊥β 其中正确命题的个数是（ ）
| A、1 | B、2 | C、3 | D、0 |
设△ABC的面积为S，已知S=a2-（b-c）2，则tan
的值为（ ）
| A |
| 2 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
函数y=Asin（ωx+φ）（A＞0，ω＞0）的部分图象如图所示，则下列正确的是（ ）
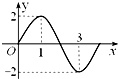
A、y=2sin
| ||
| B、y=2sinπx | ||
C、y=sin
| ||
| D、y=2sin2x |
已知tan（
+α）=3，则tanα=（ ）
| π |
| 4 |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |