题目内容
给定数列,1,2+3+4,5+6+7+8+9,10+11+12+13+14+15+16,…则这个数列的通项公式是( )
| A、an=2n2+3n-1 |
| B、an=n2+5n-5 |
| C、an=2n3-3n2+3n-1 |
| D、an=2n3-n2+n-2 |
考点:数列的函数特性
专题:探究型
分析:判断第n项的项数和第n项的最后一个数,利用第n项等于第n项与第n-1项最后一个数之差求数列的通项公式.
解答:
解:由数列知,第n项的共有2n-1项,且第n项的最后一个数为1+3+5+…+(2n-1)=
×n=n2,
∴数列的通项公式an=(1+2+3+…+n2)-[1+2+3+…+(n-1)2]=(n-1)2+1+(n-1)2+2+…+(n-1)2+(2n-1)
=(n-1)2×(2n-1)+
×(2n-1)=2n3-3n2+3n-1.
故选:C.
| 1+2n-1 |
| 2 |
∴数列的通项公式an=(1+2+3+…+n2)-[1+2+3+…+(n-1)2]=(n-1)2+1+(n-1)2+2+…+(n-1)2+(2n-1)
=(n-1)2×(2n-1)+
| 1+2n-1 |
| 2 |
故选:C.
点评:本题考查了数列的函数特性,判断第n项的项数即第n项的最后一个数是解题的关键.

练习册系列答案
相关题目
设△ABC的面积为S,已知S=a2-(b-c)2,则tan
的值为( )
| A |
| 2 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则下列正确的是( )
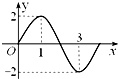

A、y=2sin
| ||
| B、y=2sinπx | ||
C、y=sin
| ||
| D、y=2sin2x |
等差数列{an}的前n项和Sn满足:S13=2184,则3(a3+a5)+2(a7+a10+a13)的值是( )
| A、2013 | B、2016 |
| C、2014 | D、不确定 |
已知数列{an}中,a1=
,an=1-
(n≥2),则a2012=( )
| 3 |
| 5 |
| 1 |
| an-1 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知tan(
+α)=3,则tanα=( )
| π |
| 4 |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
 在一个盒子中有分别标有数字0,1,2,3,4的5张卡片,现从中一次取出2张卡片,则取到的卡片上的数字之和为偶数的概率是
在一个盒子中有分别标有数字0,1,2,3,4的5张卡片,现从中一次取出2张卡片,则取到的卡片上的数字之和为偶数的概率是 如图,母线长为2的圆锥PO中,已知AB是半径为1的⊙O的直径,点C在AB弧上,D为AC的中点.
如图,母线长为2的圆锥PO中,已知AB是半径为1的⊙O的直径,点C在AB弧上,D为AC的中点.