题目内容
已知
1,
2是一对不共线向量,若
=
1+λ
2,
=-2λ
1-
2且
,
共线,则λ的值为( )
| e |
| e |
| a |
| e |
| e |
| b |
| e |
| e |
| a |
| b |
A、±
| ||||
B、±
| ||||
C、
| ||||
D、-
|
考点:平行向量与共线向量
专题:平面向量及应用
分析:用向量共线的充要条件是存在实数k,使
=k
,及向量相等坐标分别相等列方程解得.
| a |
| b |
解答:
解:∵
=
1+λ
2,
=-2λ
1-
2且
,
共线,
∴存在实数k,使
=k
,
即
1+λ
2=k(-2λ
1-
2)
∴
解得,λ±
,
故选:A
| a |
| e |
| e |
| b |
| e |
| e |
| a |
| b |
∴存在实数k,使
| a |
| b |
即
| e |
| e |
| e |
| e |
∴
|
解得,λ±
| ||
| 2 |
故选:A
点评:本题主要考查了向量共线的条件,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知复数z=-
+
i,则
=( )
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| z |
A、-
| ||||||
B、-
| ||||||
C、
| ||||||
D、
|
函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则下列正确的是( )
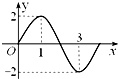

A、y=2sin
| ||
| B、y=2sinπx | ||
C、y=sin
| ||
| D、y=2sin2x |
等差数列{an}的前n项和Sn满足:S13=2184,则3(a3+a5)+2(a7+a10+a13)的值是( )
| A、2013 | B、2016 |
| C、2014 | D、不确定 |
已知数列{an}中,a1=
,an=1-
(n≥2),则a2012=( )
| 3 |
| 5 |
| 1 |
| an-1 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
下列求导运算错误的是( )
| A、x′=1 | ||
B、(log2x)′=
| ||
| C、(ex)′=ex | ||
| D、(sinx)′=cosx |
已知tan(
+α)=3,则tanα=( )
| π |
| 4 |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
已知双曲线
-
=1,(a>b>0),两渐近线的夹角为
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、2或
|
 如图在四棱锥P-ABCD中,底面ABCD是菱形,O是AC,BD的交点,PA=PC,PB=PD,E是PC上一点.求证:
如图在四棱锥P-ABCD中,底面ABCD是菱形,O是AC,BD的交点,PA=PC,PB=PD,E是PC上一点.求证: