题目内容
直角坐标系的原点为极点,x轴正半轴为极轴,单位长度不变,建立极坐标系,则曲线C:
(α为参数)的极坐标方程是 .
|
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:利用同角三角函数的基本关系把曲线C方程的参数消去,化为普通方程.再根据直角坐标和极坐标的互化公式x=ρcosθ、y=ρsinθ,把它化为极坐标方程.
解答:
解:利用同角三角函数的基本关系把曲线C:
(α为参数)的参数消去,
化为普通方程为 x2+(y-3)2=9.
再根据直角坐标和极坐标的互化公式x=ρcosθ、y=ρsinθ,
把它化为极坐标方程为(ρcosθ)2+(ρsinθ-3)2=9,化简可得ρ=6sinθ,
故答案为:ρ=6sinθ.
|
化为普通方程为 x2+(y-3)2=9.
再根据直角坐标和极坐标的互化公式x=ρcosθ、y=ρsinθ,
把它化为极坐标方程为(ρcosθ)2+(ρsinθ-3)2=9,化简可得ρ=6sinθ,
故答案为:ρ=6sinθ.
点评:本题主要考查把参数方程化为普通方程,把直角坐标方程化为极坐标方程的方法,属于基础题.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
已知复数z=-
+
i,则
=( )
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| z |
A、-
| ||||||
B、-
| ||||||
C、
| ||||||
D、
|
函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则下列正确的是( )
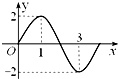

A、y=2sin
| ||
| B、y=2sinπx | ||
C、y=sin
| ||
| D、y=2sin2x |
 在一个盒子中有分别标有数字0,1,2,3,4的5张卡片,现从中一次取出2张卡片,则取到的卡片上的数字之和为偶数的概率是
在一个盒子中有分别标有数字0,1,2,3,4的5张卡片,现从中一次取出2张卡片,则取到的卡片上的数字之和为偶数的概率是