题目内容
已知p:|1-2x|≤5,q:x2-4x+4-9m2≤0(m>0).若p是q的充分不必要条件,求实数m的取值范围.
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:求出不等式对应的条件,根据充分条件和必要条件的定义进行判断.
解答:
解:因为p:|1-2x|≤5,即-2≤x≤3,
q:x2-4x+4-9m2≤0(m>0).
即[x-(2-3m)][x-(2+3m)]≤0,
即2-3m≤x≤2+3m,m>0,
若p是q的充分不必要条件,
则
且等号不能同时取得,
即
解得m≥
.
q:x2-4x+4-9m2≤0(m>0).
即[x-(2-3m)][x-(2+3m)]≤0,
即2-3m≤x≤2+3m,m>0,
若p是q的充分不必要条件,
则
|
即
|
解得m≥
| 4 |
| 3 |
点评:本题主要考查充分条件和必要条件的判断和应用,根据不等式之间的关系是解决本题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
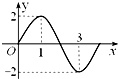
函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则下列正确的是( )

A、y=2sin
| ||
| B、y=2sinπx | ||
C、y=sin
| ||
| D、y=2sin2x |
已知tan(
+α)=3,则tanα=( )
| π |
| 4 |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
已知双曲线
-
=1,(a>b>0),两渐近线的夹角为
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、2或
|
已知x>0,y>0,且(x-1)(y-1)≥2,则x+y的取值范围是( )
| A、[3,+∞) | ||
| B、[2,+∞) | ||
C、[2
| ||
D、[
|
 如图,母线长为2的圆锥PO中,已知AB是半径为1的⊙O的直径,点C在AB弧上,D为AC的中点.
如图,母线长为2的圆锥PO中,已知AB是半径为1的⊙O的直径,点C在AB弧上,D为AC的中点. 如图在四棱锥P-ABCD中,底面ABCD是菱形,O是AC,BD的交点,PA=PC,PB=PD,E是PC上一点.求证:
如图在四棱锥P-ABCD中,底面ABCD是菱形,O是AC,BD的交点,PA=PC,PB=PD,E是PC上一点.求证: