题目内容
在△ABC中，a，b，c分别为角A，B，C所对的边，a=2，b=
，∠B=60°，则边长c= ．
| 7 |
考点：正弦定理
专题：解三角形
分析：利用余弦定理列出关系式，将a，b及cosB的值代入，得到关于c的方程，求出方程的解即可得到c的值．
解答：
解：∵a=2，b=
，B=60°，
∴由余弦定理b2=a2+c2-2accosB，即：7=4+c2-2c，即（c-3）（c+1）=0，
解得：c=3或c=-1（舍去），
则c=3．
故答案为：3
| 7 |
∴由余弦定理b2=a2+c2-2accosB，即：7=4+c2-2c，即（c-3）（c+1）=0，
解得：c=3或c=-1（舍去），
则c=3．
故答案为：3
点评：此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键，属于基本知识的考查．
练习册系列答案
导学教程高中新课标系列答案
相关题目
若A为抛物线y=
x2的顶点，过抛物线焦点的直线交抛物线于B、C两点，则
•
等于（ ）
| 1 |
| 4 |
| AB |
| AC |
| A、-3 | B、3 | C、5 | D、-5 |
命题“?x∈[-2，1]，x2-a≤0”为真命题的一个必要不充分条件是（ ）
| A、a≥4 | B、a≥1 |
| C、a≤4 | D、a≤1 |
已知正四棱锥S-ABCD中，SA=2
，那么当该棱锥的体积最大时，它的底面积为（ ）
| 3 |
| A、4 | B、8 | C、16 | D、32 |
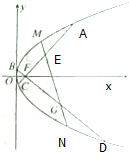如图，抛物线C：y2=2px（p＞0）的焦点F（1，0），过点F任作两条弦AC，BD，且