题目内容
已知函数f（x）=x2+2|x|-8，定义域为[a，b]（a，b∈Z），值域为[-8，0]，则满足条件的整数对（a，b）有 对．
考点：函数的值域,函数的定义域及其求法
专题：计算题,函数的性质及应用
分析：由题意确定函数的定义域的可能情况即可．
解答：
解：∵函数f（x）=x2+2|x|-8的值域为[-8，0]，
且当且仅当x=0时，f（x）=-8；
当且仅当x=±2，f（x）=0；
则满足条件的整数对（a，b）有
[-2，0]，[-2，1]，[-2，2]，[-1，2]，[0，2]；
共5对；
故答案为：5．
且当且仅当x=0时，f（x）=-8；
当且仅当x=±2，f（x）=0；
则满足条件的整数对（a，b）有
[-2，0]，[-2，1]，[-2，2]，[-1，2]，[0，2]；
共5对；
故答案为：5．
点评：本题考查了函数值域的应用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
设集合M={x|x＜2012}，N={x|0＜x≤2012}，则M∪N=（ ）
| A、M |
| B、N |
| C、{x|x≤2012} |
| D、{x|0＜x＜2012} |
下列命题正确的是（ ）
A、函数y=cos（x+
| ||||||
| B、函数y=cos4x-sin4x的最小正周期为2π | ||||||
C、函数y=sin（2x+
| ||||||
D、函数y=tan（x+
|
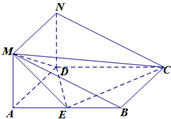如图所示的几何体中，四边形ABCD为菱形，AMND是矩形，平面AMND⊥平面ABCD，∠DAB=60°，AD=2，AM=1．
一个几何体的三视图如图所示，则该几何体的体积为（ ）
| A、4 | ||
B、4+
| ||
| C、8+π | ||
D、2+
|