题目内容
已知函数f(x)=
是定义域上的奇函数,则a+b的值为 .
| ex+a |
| ex+b |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据奇函数的定义,f(-x)=-f(x),即可解得.
解答:
解:由奇函数的性质可知:f(-x)=-f(x),
即
=-
,
∴
,
解得:
或
,
∴a+b=0
故答案为0.
即
| e-x+a |
| e-x+b |
| ex+a |
| ex+b |
∴
|
解得:
|
|
∴a+b=0
故答案为0.
点评:本题主要考查函数的奇偶性,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=sin(
x+
),则f(x)的最小正周期和初相φ分别为 ( )
| π |
| 3 |
| π |
| 6 |
A、T=6π,φ=
| ||
B、T=6π,φ=
| ||
C、T=6,φ=
| ||
D、T=6,φ=
|
下列结论成立的是( )
| A、若ac>bc,则a>b |
| B、若a>b,则a2>b2 |
| C、若a>b,c<d,则a+c>b+d |
| D、若a>b,c>d,则a-d>b-c |
已知命题p:直线m,n相交,命题q:直线m,n异面,则?p是q成立的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
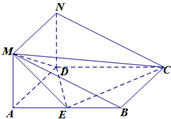 如图所示的几何体中,四边形ABCD为菱形,AMND是矩形,平面AMND⊥平面ABCD,∠DAB=60°,AD=2,AM=1.
如图所示的几何体中,四边形ABCD为菱形,AMND是矩形,平面AMND⊥平面ABCD,∠DAB=60°,AD=2,AM=1.