题目内容
求下列函数的值域:
(1)f(x)=x-2+
,x∈[-
,
);
(2)f(x)=
.
(1)f(x)=x-2+
| 1-2x |
| 9 |
| 32 |
| 3 |
| 8 |
(2)f(x)=
| ||
|
考点:函数的值域
专题:函数的性质及应用
分析:(1)令t=
,利用换元法可将函数解析式化为y═-
(t-1)2-1,根据二次函数的图象和性质可得函数的值域;
(2)由y=
得
=
≥0,根据
的有界性转化为解不等式,从而求解y的范围.
| 1-2x |
| 1 |
| 2 |
(2)由y=
| ||
|
| x |
| y+1 |
| y-1 |
| x |
解答:
解:(1)令t=
,∵x∈[-
,
),∴
<
≤
,∴
<t≤
;
则x=
(1-t2)
由函数可化为y═
(1-t2)+t-2=-
(t-1)2-1,
当t=1时,函数取最大值-1.无最大值,把t=
代入得-
,
故函数f(x)的值域是(-
,-1]
(2)由y=
得
=
≥0,
∴y≤-1或y>1,
∴故函数f(x)的值域是(-∞,-1]∪(1,+∞).
| 1-2x |
| 9 |
| 32 |
| 3 |
| 8 |
| 1 |
| 2 |
| 1-2x |
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
则x=
| 1 |
| 2 |
由函数可化为y═
| 1 |
| 2 |
| 1 |
| 2 |
当t=1时,函数取最大值-1.无最大值,把t=
| 1 |
| 2 |
| 9 |
| 8 |
故函数f(x)的值域是(-
| 9 |
| 8 |
(2)由y=
| ||
|
| x |
| y+1 |
| y-1 |
∴y≤-1或y>1,
∴故函数f(x)的值域是(-∞,-1]∪(1,+∞).
点评:本题考查的知识点是函数的值域:其中利用换元法,将问题转化为求二次函数的值域问题是解答的关键;同时,利用代数式的有界性求解范围也是常用方法.

练习册系列答案
相关题目
已知函数f(x)=alog2x+blog4x+2,且f(
)=4,则f(2014)的值为( )
| 1 |
| 2014 |
| A、-4 | B、2 | C、0 | D、-2 |
已知命题p:若2b=a+c,则a、b、c成等差数列;命题q:若b2=ac,则a、b、c成等比数列,则下列命题中是真命题的是( )
| A、¬p或q | B、p且q |
| C、¬p且¬q | D、¬p或¬q |
设Sn为等比数列{an}的前n项和,S4=1,S8=3,则S20=( )
| A、15 | B、16 | C、81 | D、31 |
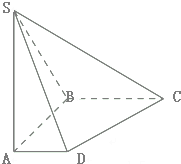 如图,四边形ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=
如图,四边形ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=