题目内容
已知函数f（x）=alog2x+blog4x+2，且f（
）=4，则f（2014）的值为（ ）
| 1 |
| 2014 |
| A、-4 | B、2 | C、0 | D、-2 |
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：利用对数的运算性质，可得f（
）+f（2014）=4，因此f（20124）=4-f（
）=0，即f（2014）的值为零．
| 1 |
| 2014 |
| 1 |
| 2014 |
解答：
解：由函数f（x）=alog2x+blog3x+2，
得f（
）=alog2
+blog3
+2=-alog2x-blog3x+2=4-（alog2x+blog3x+2），
因此f（x）+f（
）=4
再令x=2014得f（
）+f（2014）=4
所以f（2014）=4-f（
）=0，
故选：C．
得f（
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
因此f（x）+f（
| 1 |
| x |
再令x=2014得f（
| 1 |
| 2014 |
所以f（2014）=4-f（
| 1 |
| 2014 |
故选：C．
点评：本题考查了对数的运算性质，和函数的简单性质，属于基础题．利用互为倒数的两个自变量的函数值之间的关系，是解决本题的关键．
练习册系列答案
相关题目
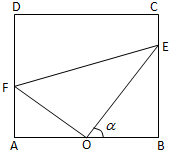合肥一中生活区内建有一块矩形休闲区域ABCD，AB=100米，BC=50