Question

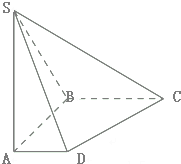如图，四边形ABCD是直角梯形，∠ABC=90°，SA⊥平面ABCD，SA=AB=BC=1，AD=

1

2

，求平面SCD的法向量．

Answer 1

考点：平面的法向量

专题：空间向量及应用

分析：建立坐标系，可得

SC

和

SD

的坐标，设平面SCD的法向量为

n

=（x，y，z），可得

n • SC =x+y-z=0 n • SD = 1 2 x-z=0

，解方程组取z=1可得一个法向量．

解答： 解：由题意，以A为原点，分别以AD、AB、AS所在直线为x、y、z轴建立坐标系，
可得S（0，0，1），D（

1

2

，0，0），C（1，1，0），
∴

SC

=（1，1，-1），

SD

=（

1

2

，0，-1），
设平面SCD的法向量为

n

=（x，y，z），
则

n • SC =x+y-z=0 n • SD = 1 2 x-z=0

，解得

x=2z y=-z

，
取z=1可得平面SCD的一个法向量为

n

=（2，-1，1），

点评：本题考查平面法向量的求解，属基础题．