题目内容
求倾斜角为45°,且与点(2,-1)的距离为
的直线方程.
| ||
| 2 |
考点:点到直线的距离公式
专题:直线与圆
分析:由题设知直线的斜率为1,设方程为y=x+b,即x-y+b=0,由直线与点(-2,-1)的距离为
,利用点到直线的距离公式求b.
| ||
| 2 |
解答:
解:∵倾斜角为45°,
∴k=tan45°=1,
∴直线的方程为y=x+b,
即x-y+b=0,
∵直线与点(2,-1)的距离为
,
∴
=
,
∴|b+3|=1
b+3=±1
b=-4,或b=-2
所以直线的方程为x-y-4=0或x-y-2=0.
∴k=tan45°=1,
∴直线的方程为y=x+b,
即x-y+b=0,
∵直线与点(2,-1)的距离为
| ||
| 2 |
∴
| |2+1+b| | ||
|
| ||
| 2 |
∴|b+3|=1
b+3=±1
b=-4,或b=-2
所以直线的方程为x-y-4=0或x-y-2=0.
点评:本题考查直线方程的求法,解题时要认真审题,注意点到直线距离公式的灵活运用.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
P是圆(x-5)2+(y-3)2=9上点,则点P到直线3x+4y-2=0的最大距离是( )
| A、2 | B、5 | C、8 | D、9 |
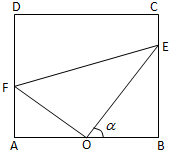 合肥一中生活区内建有一块矩形休闲区域ABCD,AB=100米,BC=50
合肥一中生活区内建有一块矩形休闲区域ABCD,AB=100米,BC=50