题目内容
设定义在D上的函数y=h(x)在点P(x0,h(x0))处的切线方程为l:y=g(x),当x≠x0时,若
>0在D内恒成立,则称P为函数y=h(x)的“类对称点”,则f(x)=x2-6x+4lnx的“类对称点”的横坐标是( )
| h(x)-g(x) |
| x-x0 |
| A、1 | ||
B、
| ||
| C、e | ||
D、
|
考点:利用导数研究曲线上某点切线方程
专题:计算题,新定义,导数的概念及应用,导数的综合应用
分析:函数y=H(x)在其图象上一点P(x0,f(x0))处的切线方程为y=g(x)=(2x0+
-6)(x-x0)++x02-6x0+4lnx0.由此能推导出y=h(x)存在“类对称点”,
是一个“类对称点”的横坐标.
| 4 |
| x0 |
| 2 |
解答:
解:函数y=h(x)在其图象上一点P(x0,h(x0))处的切线方程为:
y=g(x)=(2x0+
-6)(x-x0)+x02-6x0+4lnx0,
设m(x)=h(x)-g(x)=x2-6x+4lnx-(2x0+
-6)(x-x0)-x02+6x0-4lnx0,
则m(x0)=0.
m′(x)=2x+
-6-(2x0+
-6)=2(x-x0)(1-
)=
(x-x0)(x-
)
若x0<
,φ(x)在(x0,
)上单调递减,
∴当x∈(x0,
)时,m(x)<m(x0)=0,此时
<0;
若x0>
,φ(x)在(
,x0)上单调递减,
∴当x∈(
,x0)时,m(x)>m(x0)=0,此时
<0;
∴y=h(x)在(0,
)∪(
,+∞)上不存在“类对称点”.
若x0=
,
(x-
)2>0,
∴m(x)在(0,+∞)上是增函数,
当x>x0时,m(x)>m(x0)=0,
当x<x0时,m(x)<m(x0)=0,故
>0.
即此时点P是y=f(x)的“类对称点”
综上,y=h(x)存在“类对称点”,
是一个“类对称点”的横坐标.
故选B.
y=g(x)=(2x0+
| 4 |
| x0 |
设m(x)=h(x)-g(x)=x2-6x+4lnx-(2x0+
| 4 |
| x0 |
则m(x0)=0.
m′(x)=2x+
| 4 |
| x |
| 4 |
| x0 |
| 2 |
| xx0 |
| 2 |
| x |
| 2 |
| x0 |
若x0<
| 2 |
| 2 |
| x0 |
∴当x∈(x0,
| 2 |
| x0 |
| m(x) |
| x-x0 |
若x0>
| 2 |
| 2 |
| x0 |
∴当x∈(
| 2 |
| x0 |
| m(x) |
| x-x0 |
∴y=h(x)在(0,
| 2 |
| 2 |
若x0=
| 2 |
| 2 |
| x |
| 2 |
∴m(x)在(0,+∞)上是增函数,
当x>x0时,m(x)>m(x0)=0,
当x<x0时,m(x)<m(x0)=0,故
| m(x) |
| x-x0 |
即此时点P是y=f(x)的“类对称点”
综上,y=h(x)存在“类对称点”,
| 2 |
故选B.
点评:本题考查函数的单调增区间的求法,探索满足函数在一定零点下的参数的求法,探索函数是否存在“类对称点”.解题时要认真审题,注意分类讨论思想和等价转化思想的合理运用,此题是难题.

练习册系列答案
相关题目
抛物线y=mx2的焦点与椭圆
+
=1的上焦点重合,则m=( )
| y2 |
| 6 |
| x2 |
| 2 |
A、
| ||
B、
| ||
| C、8 | ||
| D、4 |
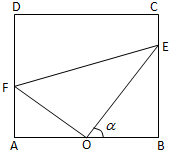 合肥一中生活区内建有一块矩形休闲区域ABCD,AB=100米,BC=50
合肥一中生活区内建有一块矩形休闲区域ABCD,AB=100米,BC=50 如图,P为△ABC所在平面外一点,PA⊥PB,PB⊥PC,PC⊥PA,PH⊥平面ABC于H,求证:H是△ABC的垂心,△ABC为锐角三角形.
如图,P为△ABC所在平面外一点,PA⊥PB,PB⊥PC,PC⊥PA,PH⊥平面ABC于H,求证:H是△ABC的垂心,△ABC为锐角三角形.