题目内容
已知命题p：若2b=a+c，则a、b、c成等差数列；命题q：若b2=ac，则a、b、c成等比数列，则下列命题中是真命题的是（ ）
| A、￢p或q | B、p且q |
| C、￢p且￢q | D、￢p或￢q |
考点：复合命题的真假
专题：简易逻辑
分析：首先，判断命题p为真命题，命题q为假命题，然后，结合复合命题的真值表进行判断即可．
解答：
解：命题p：若2b=a+c，则a、b、c成等差数列，
该为真命题；
对于命题q：若b2=ac，
不妨取a=b=c=0，
显然满足题意，但是不是等比数列，
故该命题为假命题．
∴￢p或q为假命题；
p且q为假命题；
￢p且￢q为假命题，
￢p或￢q为真命题，
故选：D．
该为真命题；
对于命题q：若b2=ac，
不妨取a=b=c=0，
显然满足题意，但是不是等比数列，
故该命题为假命题．
∴￢p或q为假命题；
p且q为假命题；
￢p且￢q为假命题，
￢p或￢q为真命题，
故选：D．
点评：本题重点考查了命题的真假判断、复合命题的真假判断等知识，属于中档题，解题关键是准确判断所给的两个命题的真假情况．
练习册系列答案
相关题目
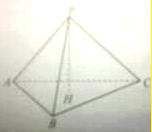如图，P为△ABC所在平面外一点，PA⊥PB，PB⊥PC，PC⊥PA，PH⊥平面ABC于H，求证：H是△ABC的垂心，△ABC为锐角三角形．