题目内容
设{an}是由正数组成的等比数列，Sn为其前n项和，已知a2a4=81，S3=13，则S5等于（ ）
| A、40 | B、81 |
| C、121 | D、243 |
考点：等比数列的前n项和
专题：等差数列与等比数列
分析：设等比数列{an}的公比为q，由等比数列的通项公式、前n项和公式列出方程，结合条件求出公比和首项，利用等比数列的前n项和公式求出S5．
解答：
解：设等比数列{an}的公比为q，且q＞0，
因为a2a4=81，S3=13，所以
，
又{an}是由正数组成的等比数列，则解得
，
所以S5=
=121，
故选：C．
因为a2a4=81，S3=13，所以
|
又{an}是由正数组成的等比数列，则解得
|
所以S5=
| 1-35 |
| 1-3 |
故选：C．
点评：本题考查等比数列的通项公式、前n项和公式，以及方程思想，考查化简计算能力，注意条件的应用．
练习册系列答案
阶梯计算系列答案
相关题目
为了解甲、乙两个班级某次考试的数学成绩（单位：分），从甲、乙两个班级中分别随机抽取5名学生的成绩作标本，如图是样本的茎叶图，规定：成绩不低于120分时为优秀成绩．关于幂函数f（x）=x3，若0＜x1＜x2，则f（
）、
的大小关系（ ）
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
A、f（
| ||||
B、f（
| ||||
C、f（
| ||||
| D、无法确定 |
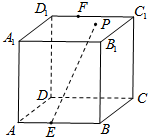如图，已知正方体ABCD-A1B1C1D1的棱长为4，点E，F分别是线段AB，C1D1上的动点，点P是上底面A1B1C1D1内一动点，且满足点P到点F的距离等于点P到平面ABB1A1的距离，则当点P运动时，PE的最小值是（ ）
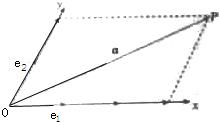如图，设Ox、Oy是平面内相交成60°角的两条数轴，