题目内容
如图,正方体ABCD-A1B1C1D1中,M∈AA1,N∈AB,∠C1MN=90°,B1N=2MN,则∠MNB1= .


考点:空间向量的夹角与距离求解公式
专题:空间角
分析:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出∠MNB1的大小.
解答:
 解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,
建立空间直角坐标系,
设M(1,0,b),N(1,a,0),A(1,0,0),B(1,1,0),
B1(1,1,1),C1(0,1,1),
=(1,-1,b-1),
=(0,a,-b),
=(0,a-1,-1),
∵∠C1MN=90°,B1N=2MN,
∴
•
=-a+b(1-b)=0,∴a=b(1-b),
∴cos∠MNB1=
=
=
=
,
∴∠MNB1=60°.
故答案为:60°.
 解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设M(1,0,b),N(1,a,0),A(1,0,0),B(1,1,0),
B1(1,1,1),C1(0,1,1),
| C1M |
| MN |
| B1N |
∵∠C1MN=90°,B1N=2MN,
∴
| C1M |
| MN |
∴cos∠MNB1=
| ||||
|
|
| a2-a+b |
| 2(a2+b2) |
=
| b2(1-b2)+b2 |
| 2[b2(1-b2)+b2] |
| 1 |
| 2 |
∴∠MNB1=60°.
故答案为:60°.
点评:本题考查空间角的求法,是中档题,解题时要认真审题,注意空间思维能力和向量法的合理运用.

练习册系列答案
相关题目
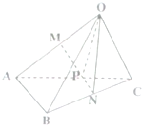 如图,M,N分别是四面体OABC的棱OA,BC的中点,点P在MN上且满足
如图,M,N分别是四面体OABC的棱OA,BC的中点,点P在MN上且满足| MP |
| 2 |
| 3 |
| MN |
| OA |
| a |
| OB |
| b |
| OC |
| c |
| OP |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
设{an}是由正数组成的等比数列,Sn为其前n项和,已知a2a4=81,S3=13,则S5等于( )
| A、40 | B、81 |
| C、121 | D、243 |
 如图,已知AB⊥平面ACD,DE⊥平面ACD,AC=AD=4,DE=2AB=6,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,AC=AD=4,DE=2AB=6,F为CD的中点.