题目内容
在△ABC中,最长边上的中线长为15,其他两边之和为42,且sinC=
,求BC的边长.
| sinA |
| cosB |
考点:余弦定理
专题:解三角形
分析:sinC=
,由cosB=
<1,可得最长边为c或b.当最长边为c时,a+b=42,在△BCD中,由余弦定理可得:cosB=
=
,解得c.在△ABC中,由余弦定理可得:cosB=
=
,联立解出即可.当最长边为b时.经过计算,不符合题意,舍去.
| sinA |
| cosB |
| a |
| c |
(
| ||
2×
|
| a |
| c |
| a2+c2-b2 |
| 2ac |
| a |
| c |
解答:
解:∵sinC=
,∴cosB=
<1,
∴最长边为c或b.
①当最长边为c时,a+b=42,
在△BCD中,由余弦定理可得:cosB=
=
,解得c=30.
在△ABC中,由余弦定理可得:cosB=
=
,化为c2=b2+a2,又c=30,a+b=42,解得a=24或18.
②当最长边为b时.经过计算,不符合题意,舍去.
综上可得:BC=24或18.
| sinA |
| cosB |
| a |
| c |

∴最长边为c或b.
①当最长边为c时,a+b=42,
在△BCD中,由余弦定理可得:cosB=
(
| ||
2×
|
| a |
| c |
在△ABC中,由余弦定理可得:cosB=
| a2+c2-b2 |
| 2ac |
| a |
| c |
②当最长边为b时.经过计算,不符合题意,舍去.
综上可得:BC=24或18.
点评:本题考查了正弦定理、余弦定理、分类讨论思想方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
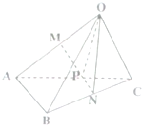 如图,M,N分别是四面体OABC的棱OA,BC的中点,点P在MN上且满足
如图,M,N分别是四面体OABC的棱OA,BC的中点,点P在MN上且满足| MP |
| 2 |
| 3 |
| MN |
| OA |
| a |
| OB |
| b |
| OC |
| c |
| OP |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
设{an}是由正数组成的等比数列,Sn为其前n项和,已知a2a4=81,S3=13,则S5等于( )
| A、40 | B、81 |
| C、121 | D、243 |
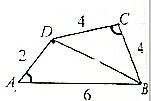 已知在四边形ABCD中,∠BAD+∠BCD=π,AB=6,BC=CD=4,AD=2,求BD的长.
已知在四边形ABCD中,∠BAD+∠BCD=π,AB=6,BC=CD=4,AD=2,求BD的长.