题目内容
 为了解甲、乙两个班级某次考试的数学成绩(单位:分),从甲、乙两个班级中分别随机抽取5名学生的成绩作标本,如图是样本的茎叶图,规定:成绩不低于120分时为优秀成绩.
为了解甲、乙两个班级某次考试的数学成绩(单位:分),从甲、乙两个班级中分别随机抽取5名学生的成绩作标本,如图是样本的茎叶图,规定:成绩不低于120分时为优秀成绩.(1)从甲班的样本中有放回的随机抽取 2 个数据,求其中只有一个优秀成绩的概率;
(2)从甲、乙两个班级的样本中分别抽取2名同学的成绩,记获优秀成绩的人数为X,求X的分布列和数学期望E(X)
考点:离散型随机变量的期望与方差,茎叶图
专题:概率与统计
分析:(1)甲班抽取的5名学生的成绩为102,112,117,124,136,从中有放回地抽取两个数据,基本事件总数n=52=25,其中只有一个优秀成绩,包含的基本事件个数m=2×3+3×2=12,由此利用等可能事件概率计算公式能求出其中只有一个优秀成绩的概率.
(2)由茎叶图知甲班抽取的5名学生中有2名学生成绩优秀,乙班抽取的5名学生中有1名学生成绩优秀,由此得X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和数学期望E(X).
(2)由茎叶图知甲班抽取的5名学生中有2名学生成绩优秀,乙班抽取的5名学生中有1名学生成绩优秀,由此得X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和数学期望E(X).
解答:
解:(1)甲班抽取的5名学生的成绩为102,112,117,124,136,
从中有放回地抽取两个数据,基本事件总数n=52=25,
其中只有一个优秀成绩,包含的基本事件个数m=2×3+3×2=12,
∴其中只有一个优秀成绩的概率p=
=
.
(2)由茎叶图知甲班抽取的5名学生中有2名学生成绩优秀,
乙班抽取的5名学生中有1名学生成绩优秀,
由此得X的可能取值为0,1,2,3,
P(X=0)=
×
=
,
P(X=1)=
×
+
×
=
,
P(X=2)=
×
+
×
=
,
P(X=3)=
×
=
,
∴X的分布列为:
EX=0×
+1×
+2×
+3×
=
.
从中有放回地抽取两个数据,基本事件总数n=52=25,
其中只有一个优秀成绩,包含的基本事件个数m=2×3+3×2=12,
∴其中只有一个优秀成绩的概率p=
| m |
| n |
| 12 |
| 25 |
(2)由茎叶图知甲班抽取的5名学生中有2名学生成绩优秀,
乙班抽取的5名学生中有1名学生成绩优秀,
由此得X的可能取值为0,1,2,3,
P(X=0)=
| ||
|
| ||
|
| 18 |
| 100 |
P(X=1)=
| ||||
|
| ||
|
| ||
|
| ||||
|
| 48 |
| 100 |
P(X=2)=
| ||||
|
| ||||
|
| ||
|
| ||
|
| 30 |
| 100 |
P(X=3)=
| ||
|
| ||||
|
| 4 |
| 100 |
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 18 |
| 100 |
| 48 |
| 100 |
| 30 |
| 100 |
| 4 |
| 100 |
| 6 |
| 5 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
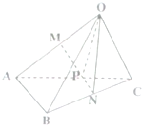 如图,M,N分别是四面体OABC的棱OA,BC的中点,点P在MN上且满足
如图,M,N分别是四面体OABC的棱OA,BC的中点,点P在MN上且满足| MP |
| 2 |
| 3 |
| MN |
| OA |
| a |
| OB |
| b |
| OC |
| c |
| OP |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
设{an}是由正数组成的等比数列,Sn为其前n项和,已知a2a4=81,S3=13,则S5等于( )
| A、40 | B、81 |
| C、121 | D、243 |
已知α为锐角,且cos(α+
)=
,则sinα为( )
| π |
| 6 |
| 3 |
| 5 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、
|
P是双曲线
-
=1(a>0,b>0)的右支上的一点,F1,F2分别是左、右焦点,则△PF1F2的内切圆圆心的横坐标为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、a | ||
| B、b | ||
C、
| ||
D、a+b-
|