题目内容
20.已知实数x,y满足约束条件$\left\{\begin{array}{l}{x-y+1≥0}\\{4x+3y-12≤0}\\{y-2≥0}\end{array}\right.$,则z=$\frac{3x-y+2}{x+1}$的最大值为( )| A. | $\frac{9}{5}$ | B. | $\frac{3}{2}$ | C. | $\frac{25}{16}$ | D. | $\frac{9}{4}$ |
分析 利用分式函数的性质,转化为直线的斜率,利用数形结合即可得到结论.
解答 解:由约束条件得到可行域如图:则z=$\frac{3x-y+2}{x+1}$=3-$\frac{y+1}{x+1}$,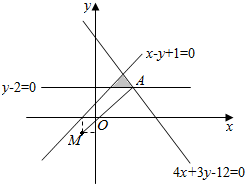 则z的几何意义是区域内的点到定点M(-1,-1)的斜率的最小值的相反数与3的和,
则z的几何意义是区域内的点到定点M(-1,-1)的斜率的最小值的相反数与3的和,
由图象可知区域边界点A(1.5,2)连接的直线斜率最小为$\frac{6}{5}$,所以z的最大值为3-$\frac{6}{5}$=$\frac{9}{5}$;
故选:A.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,关键是把目标函数变形,是中档题.

练习册系列答案
相关题目
11.如图,该算法输出的结果是( )


| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
8.设F1,F2分别是椭圆$E:{x^2}+\frac{y^2}{b^2}=1(0<b<1)$的左、右焦点,已知点F1的直线交椭圆E于A,B两点,若|AF1|=2|BF1|,AF2⊥x轴,则椭圆E的方程为( )
| A. | ${x^2}+\frac{{3{y^2}}}{2}=1$ | B. | ${x^2}+\frac{{6{y^2}}}{5}=1$ | C. | ${x^2}+\frac{{5{y^2}}}{4}=1$ | D. | ${x^2}+\frac{{8{y^2}}}{7}=1$ |
15.复数z满足z(1-i)=-1-i,则|z+2|=( )
| A. | 3 | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{5}$ |
5.过三个点A(1,3),B(4,2),C(1,-1)的圆交y轴于M,N两点,则|MN|=( )
| A. | 2$\sqrt{6}$ | B. | 3$\sqrt{6}$ | C. | 2 | D. | 5$\sqrt{6}$ |
12.在区间(1,2)内随机取个实数a,则直线y=2x,直线x=a与x轴围成的面积大于$\frac{16}{9}$的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
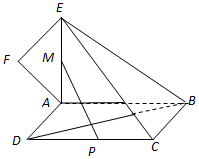 如图,正方形ABCD所在平面与四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°.
如图,正方形ABCD所在平面与四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°.